
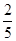 和
和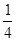 的体积露出液面。
的体积露出液面。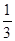 的体积露出液面,且该圆柱体底面所受液体压强为800Pa。求此时圆柱体B对地面的压强为多少?
的体积露出液面,且该圆柱体底面所受液体压强为800Pa。求此时圆柱体B对地面的压强为多少?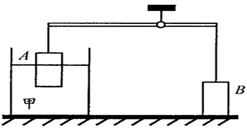

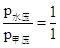 .
.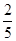 )V=ρ甲g(1-
)V=ρ甲g(1-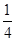 )V,∴ρ甲=
)V,∴ρ甲=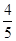 ρ水=
ρ水=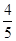 ×1×103kg/m3=0.8×103kg/m3,
×1×103kg/m3=0.8×103kg/m3,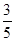 ρ水=
ρ水=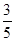 ×1×103kg/m3=0.6×103kg/m3,∵圆柱体A在液体甲中时底面所受压强为800Pa.∴h甲′=
×1×103kg/m3=0.6×103kg/m3,∵圆柱体A在液体甲中时底面所受压强为800Pa.∴h甲′=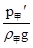 =0.1m,∵圆柱体A有
=0.1m,∵圆柱体A有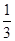 的体积露出液面,即:h甲′=(1-
的体积露出液面,即:h甲′=(1-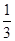 )hA,∴hA=
)hA,∴hA= h甲′=
h甲′= ×0.1m=0.15m;
×0.1m=0.15m;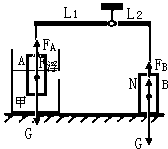
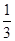 )V-2ρAgV=2gV(ρ甲-ρA)
)V-2ρAgV=2gV(ρ甲-ρA)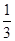 )V-2ρAgV,
)V-2ρAgV,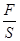 =2gh(ρ甲-ρA)=2×10N/kg×0.15m×(0.8×103kg/m3-0.6×103kg/m3)=600Pa.
=2gh(ρ甲-ρA)=2×10N/kg×0.15m×(0.8×103kg/m3-0.6×103kg/m3)=600Pa.

科目:初中物理 来源:不详 题型:填空题

查看答案和解析>>
科目:初中物理 来源:不详 题型:单选题
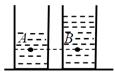
| A.pA>pB | B.pA<pB | C.pA=pB | D.无法确定 |
查看答案和解析>>
科目:初中物理 来源:不详 题型:单选题

| A.与液体高度有关 | B.与液体深度有关 |
| C.与液体质量有关 | D.与液体体积有关 |
查看答案和解析>>
科目:初中物理 来源:不详 题型:计算题

查看答案和解析>>
科目:初中物理 来源:不详 题型:实验题
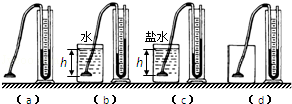
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com