
 如图是某公共厕所的自动冲水装置原理图.浮子A是边长为20cm的正方体,盖片B的质量为1kg,表面积为100cm2,厚度不计.连接A、B的是长为20cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮子A时,盖片B被拉开,水通过排水管冲洗厕所(水的密度为1×103kg/m3,g取10N/kg).求:
如图是某公共厕所的自动冲水装置原理图.浮子A是边长为20cm的正方体,盖片B的质量为1kg,表面积为100cm2,厚度不计.连接A、B的是长为20cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮子A时,盖片B被拉开,水通过排水管冲洗厕所(水的密度为1×103kg/m3,g取10N/kg).求: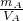 =
=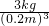 =375kg/m3.
=375kg/m3.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中物理 来源: 题型:
 (2010?贵港)如图是某公共厕所的自动冲水装置原理图.浮子A是边长为20cm的正方体,盖片B的质量为lkg,表面积为100cm2,厚度不计.连接A、B的是长为20cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮子A时,盖片B被拉开,水通过排水管冲洗厕所(水的密度为1×103kg/m3,g取10N/kg).求:
(2010?贵港)如图是某公共厕所的自动冲水装置原理图.浮子A是边长为20cm的正方体,盖片B的质量为lkg,表面积为100cm2,厚度不计.连接A、B的是长为20cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮子A时,盖片B被拉开,水通过排水管冲洗厕所(水的密度为1×103kg/m3,g取10N/kg).求:查看答案和解析>>
科目:初中物理 来源: 题型:
 如图是某公共厕所的自动冲水装置.浮筒A是边长为20cm的正方体,盖片B的质量为lkg,表面积为80cm2,厚度不计.连接AB的是长为30cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮筒A时,水对盖片B的压力是40N,盖片B被拉开,水通过排水管流出冲洗厕所(g取10N/kg).浮筒A的质量是多少?
如图是某公共厕所的自动冲水装置.浮筒A是边长为20cm的正方体,盖片B的质量为lkg,表面积为80cm2,厚度不计.连接AB的是长为30cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮筒A时,水对盖片B的压力是40N,盖片B被拉开,水通过排水管流出冲洗厕所(g取10N/kg).浮筒A的质量是多少?查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 如图是某公共厕所的自动冲水装置.浮筒A是边长为20cm的正方体,盖片B的质量为lkg,表面积为80cm2,厚度不计.连接AB的是长为30cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮筒A时,水对盖片B的压力是40N,盖片B被拉开,水通过排水管流出冲洗厕所(g取10N/kg).浮筒A的质量是多少?
如图是某公共厕所的自动冲水装置.浮筒A是边长为20cm的正方体,盖片B的质量为lkg,表面积为80cm2,厚度不计.连接AB的是长为30cm,体积和质量都不计的硬杆.当供水管流进水箱的水刚好浸没浮筒A时,水对盖片B的压力是40N,盖片B被拉开,水通过排水管流出冲洗厕所(g取10N/kg).浮筒A的质量是多少?查看答案和解析>>
科目:初中物理 来源:《14.5 浮力》2011年同步练习(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com