
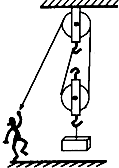
 小军利用如图的滑轮组提升货物,摩擦与绳重不计,货物质量为50kg,g=10N/kg.
小军利用如图的滑轮组提升货物,摩擦与绳重不计,货物质量为50kg,g=10N/kg.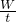 =
= =260W;
=260W; =
= =96.2%;
=96.2%; ,当G物=500N时,F=260N,则G动=20N,
,当G物=500N时,F=260N,则G动=20N,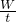 可求出功率;已知货物重力已求出,根据W有用=Gh可求出有用功,W总=FS求出总功,最后根据η=
可求出功率;已知货物重力已求出,根据W有用=Gh可求出有用功,W总=FS求出总功,最后根据η= 可求出机械效率;
可求出机械效率; ,求出动滑轮重力,再求将质量为80kg的另一个货物匀速提升3m,做的有用功W有用=G′h′,额外功W外=G动h′,最后根据W总=W有用+W外求出总功.
,求出动滑轮重力,再求将质量为80kg的另一个货物匀速提升3m,做的有用功W有用=G′h′,额外功W外=G动h′,最后根据W总=W有用+W外求出总功. ,也是只在这种情况下成立,同时还要注意同一个滑轮组如果提升的重物不同,其机械效率也不同.
,也是只在这种情况下成立,同时还要注意同一个滑轮组如果提升的重物不同,其机械效率也不同. 

科目:初中物理 来源: 题型:
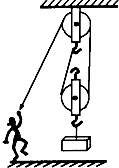 小军利用如图的滑轮组提升货物,摩擦与绳重不计,货物质量为50kg,g=10N/kg.
小军利用如图的滑轮组提升货物,摩擦与绳重不计,货物质量为50kg,g=10N/kg.查看答案和解析>>
科目:初中物理 来源: 题型:
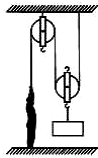 如图所示,小军利用滑轮组先后竖直向上匀速提升物体A和物体B.已知小军的质量为65kg,物体A的质量为90kg,物体B的质量为50kg.假设在拉绳子的过程中,小民对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,不计绳重和摩擦.当提升物体A时,滑轮组的机械效率为75%,求提升物体B时,滑轮组的机械效率和小军对地面的压力.(g取10N/kg)
如图所示,小军利用滑轮组先后竖直向上匀速提升物体A和物体B.已知小军的质量为65kg,物体A的质量为90kg,物体B的质量为50kg.假设在拉绳子的过程中,小民对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,不计绳重和摩擦.当提升物体A时,滑轮组的机械效率为75%,求提升物体B时,滑轮组的机械效率和小军对地面的压力.(g取10N/kg)查看答案和解析>>
科目:初中物理 来源: 题型:
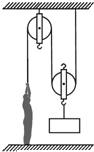 (2009?昌平区一模)小军利用滑轮组竖直向上匀速提升物体,如图所示,第一次提升时,滑轮组的机械效率为75%,小军对地面的压力为F1;第二次提升时,将物体完全浸没在某种液体中匀速提升,小军对地面的压力为F2,F1:F2=1:4,已知小军的质量为70kg,提升的物体质量为90kg,假设在拉绳子的过程中,小军对绳子的拉力与地面的压力始终竖直向下,且在同一直线上,不计绳重和摩擦,g取10N/kg,则第二次浸没在液体中匀速提升时,液体对物体的浮力大小是
(2009?昌平区一模)小军利用滑轮组竖直向上匀速提升物体,如图所示,第一次提升时,滑轮组的机械效率为75%,小军对地面的压力为F1;第二次提升时,将物体完全浸没在某种液体中匀速提升,小军对地面的压力为F2,F1:F2=1:4,已知小军的质量为70kg,提升的物体质量为90kg,假设在拉绳子的过程中,小军对绳子的拉力与地面的压力始终竖直向下,且在同一直线上,不计绳重和摩擦,g取10N/kg,则第二次浸没在液体中匀速提升时,液体对物体的浮力大小是查看答案和解析>>
科目:初中物理 来源: 题型:解答题
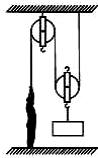 如图所示,小军利用滑轮组先后竖直向上匀速提升物体A和物体B.已知小军的质量为65kg,物体A的质量为90kg,物体B的质量为50kg.假设在拉绳子的过程中,小民对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,不计绳重和摩擦.当提升物体A时,滑轮组的机械效率为75%,求提升物体B时,滑轮组的机械效率和小军对地面的压力.(g取10N/kg)
如图所示,小军利用滑轮组先后竖直向上匀速提升物体A和物体B.已知小军的质量为65kg,物体A的质量为90kg,物体B的质量为50kg.假设在拉绳子的过程中,小民对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,不计绳重和摩擦.当提升物体A时,滑轮组的机械效率为75%,求提升物体B时,滑轮组的机械效率和小军对地面的压力.(g取10N/kg)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com