
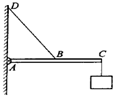
 如图所示,重力为20N的物体挂在水平横杆的右端C点.水平横杆左端有一可转动的固定轴A,轻杆AC长为1m.轻绳的B端可固定在AC 杆上的任一点,绳的D端可固定在竖直墙面上的任一点,绳BD长为1m,轻杆AC始终保持水平.则当AB间的距离为________m时(保留两位小数).绳BD的拉力最小值为________N.
如图所示,重力为20N的物体挂在水平横杆的右端C点.水平横杆左端有一可转动的固定轴A,轻杆AC长为1m.轻绳的B端可固定在AC 杆上的任一点,绳的D端可固定在竖直墙面上的任一点,绳BD长为1m,轻杆AC始终保持水平.则当AB间的距离为________m时(保留两位小数).绳BD的拉力最小值为________N. =0.5m,所以底边AB=
=0.5m,所以底边AB= ×0.5m≈0.71m.
×0.5m≈0.71m.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com