
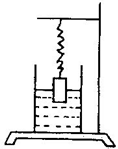
 一个密度为2×103千克/米3的圆柱体高10厘米,用一根弹簧把它吊起来,让它的一半浸没在水中(盛水的容器很大),此时弹簧比原长伸长了8厘米(已知弹簧的伸长量与所受的拉力成正比,即F=k△x,k对给定的弹簧来说是常数,△x是弹簧的伸长量),现再往容器中注入密度为0.8×103千克/米3的油,并超过圆柱顶.问此时弹簧的伸长是多少?
一个密度为2×103千克/米3的圆柱体高10厘米,用一根弹簧把它吊起来,让它的一半浸没在水中(盛水的容器很大),此时弹簧比原长伸长了8厘米(已知弹簧的伸长量与所受的拉力成正比,即F=k△x,k对给定的弹簧来说是常数,△x是弹簧的伸长量),现再往容器中注入密度为0.8×103千克/米3的油,并超过圆柱顶.问此时弹簧的伸长是多少? h=kx1------------①
h=kx1------------① h-(x1-x2)]-ρ油gS[
h-(x1-x2)]-ρ油gS[ h+(x1-x2)]=kx2--------②
h+(x1-x2)]=kx2--------② =
=
 ×103kg/m3×0.1m)x2=[2×103kg/m3×0.1m-
×103kg/m3×0.1m)x2=[2×103kg/m3×0.1m- ×103kg/m3×0.1m+103kg/m3×(0.08m-x2)-
×103kg/m3×0.1m+103kg/m3×(0.08m-x2)- ×800kg/m3×0.1m-800kg/m3×(0.08m-x2)]×0.08m
×800kg/m3×0.1m-800kg/m3×(0.08m-x2)]×0.08m

科目:初中物理 来源: 题型:
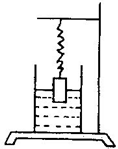 一个密度为2×103千克/米3的圆柱体高10厘米,用一根弹簧把它吊起来,让它的一半浸没在水中(盛水的容器很大),此时弹簧比原长伸长了8厘米(已知弹簧的伸长量与所受的拉力成正比,即F=k△x,k对给定的弹簧来说是常数,△x是弹簧的伸长量),现再往容器中注入密度为0.8×103千克/米3的油,并超过圆柱顶.问此时弹簧的伸长是多少?
一个密度为2×103千克/米3的圆柱体高10厘米,用一根弹簧把它吊起来,让它的一半浸没在水中(盛水的容器很大),此时弹簧比原长伸长了8厘米(已知弹簧的伸长量与所受的拉力成正比,即F=k△x,k对给定的弹簧来说是常数,△x是弹簧的伸长量),现再往容器中注入密度为0.8×103千克/米3的油,并超过圆柱顶.问此时弹簧的伸长是多少?查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com