
 如图所示,是日杂货店中常用的电子秤内部结构示意图,E为电源,电压为3V;Ro为定值电阻,Ro=1000Ω,A为劲度系数等于20N/cm的轻质弹簧,在弹性限度内它的最大压缩量为4.1cm,B为滑动变阻器,P为滑动触头(摩擦可以忽略不计),放上支架托盘C后,弹簧刚好缩短了1mm,这时,触头P刚好触在滑动变阻器最上端,安培表示数为1mA.当称量质量为2kg的大米时,安培表示数为1.2mA.已知,导体电阻的大小跟导体的长度成正比,滑动变阻器有效长度为4cm,如图
如图所示,是日杂货店中常用的电子秤内部结构示意图,E为电源,电压为3V;Ro为定值电阻,Ro=1000Ω,A为劲度系数等于20N/cm的轻质弹簧,在弹性限度内它的最大压缩量为4.1cm,B为滑动变阻器,P为滑动触头(摩擦可以忽略不计),放上支架托盘C后,弹簧刚好缩短了1mm,这时,触头P刚好触在滑动变阻器最上端,安培表示数为1mA.当称量质量为2kg的大米时,安培表示数为1.2mA.已知,导体电阻的大小跟导体的长度成正比,滑动变阻器有效长度为4cm,如图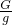 =
= =8kg,
=8kg,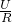 可得:
可得: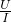 =
=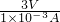 =3000Ω,
=3000Ω,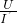 =
=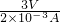 =1500Ω,
=1500Ω,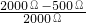 ×4cm=3cm,
×4cm=3cm,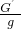 =
=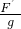 =
=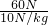 =6kg.
=6kg.

科目:初中物理 来源: 题型:
 如图所示,是日杂货店中常用的电子秤内部结构示意图,E为电源,电压为3V;Ro为定值电阻,Ro=1000Ω,A为劲度系数等于20N/cm的轻质弹簧,在弹性限度内它的最大压缩量为4.1cm,B为滑动变阻器,P为滑动触头(摩擦可以忽略不计),放上支架托盘C后,弹簧刚好缩短了1mm,这时,触头P刚好触在滑动变阻器最上端,安培表示数为1mA.当称量质量为2kg的大米时,安培表示数为1.2mA.已知,导体电阻的大小跟导体的长度成正比,滑动变阻器有效长度为4cm,如图
如图所示,是日杂货店中常用的电子秤内部结构示意图,E为电源,电压为3V;Ro为定值电阻,Ro=1000Ω,A为劲度系数等于20N/cm的轻质弹簧,在弹性限度内它的最大压缩量为4.1cm,B为滑动变阻器,P为滑动触头(摩擦可以忽略不计),放上支架托盘C后,弹簧刚好缩短了1mm,这时,触头P刚好触在滑动变阻器最上端,安培表示数为1mA.当称量质量为2kg的大米时,安培表示数为1.2mA.已知,导体电阻的大小跟导体的长度成正比,滑动变阻器有效长度为4cm,如图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com