声源振动时发出声音的频率即为每秒钟发出声波的数目,声源每秒钟发出的波数不同,发出声音的频率就不同.对观察者而言,人耳听到的声音频率即为每秒钟接收到的声波数目,例如我们听到频率为50Hz的声音,每秒钟接收到的声波数即为50.当声源靠近或远离观察者时,人耳听到的频率不再等于声源发出的频率,这种现象叫多普勒效应.
(1)我们在生活中经常有这样的经验:高速驶来的火车“呼啸而来,扬长而去”.试定性分析当火车靠近我们时,我们听到的鸣笛声与火车发出的声音频率相比有何不同?
(2)观察者静止在路旁,一列动车以速度v向观察者驶来,动车发出的鸣笛声频率为f,观察者听到的声音频率为f,声音的速度为u,试推导f与f的关系.
(3)利用多普勒效应可以测定动车的速度.观察者坐在速度为80km/h的普通列车上,从对面开来一列动车,迎面时听到动车鸣笛声的频率为f1,动车向后奔驰而去时听到的频率为f2,若f1:f2=2:1,声音的速度为1200km/h,求动车的速度大小.
【答案】
分析:(1)首先阅读材料,通过材料中得出当物体的振动频率不变时,当人耳和物声源之间发生相对运动时,人耳感知声音的音调是不同的,距离声源越远,音调越低,距离声源越近,音调越高.
(2)根据波速u列出时间t内通过的完全波的个数,从而得出接收的频率;当波源朝向观察者以速度v运动,由于波长变短,从而使单位时间内通过波的个数增多,得出f=
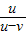
f
即可.
(3)设普通列车速度为v
1,动车的速度为v
2,声速为u,动车发出声波的频率为f,分别列出靠近时和远离时的关系式,结合f
1:f
2=2:1,解方程即可.
解答:解:(1)当声源靠近观察者时,人耳听到的鸣笛声的频率比火车发出的声音要大.因为相同时间内,人耳接收到的波数比火车发出的波数要多.反之,当声源远离观察者时,人耳听到的鸣笛声的频率比火车发出的声音要小.
当火车靠近我们时,距离越来越近,人感知的音调逐渐变高,即听到的声音频率增大了.
故答案为:听到的声音频率增大了.
(2)当波以速度u通过接收者时,时间t内通过的完全波的个数为n=,因而单位时间内通过接收者的完全波的个数,即接收的频率为f=.
波源朝向观察者以速度v运动,由于波长变短为λ
=λ-vt,而使得单位时间内通过波的个数增多,即f
═,(动车的速度小于声速)
故答案为:f=n′=f
(3)设普通列车速度为v
1,动车的速度为v
2,声速为u,动车发出声波的频率为f,则由题意可得:
靠近时:f
1=f×
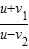
,
远离时:f
2=f×
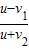
,
又因为:f
1:f
2=2:1
由上三式可得:u
2-2(v
1+v
2)u+v
1v
2=0
解得:v
2=
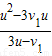
=327.3km/h.
答:动车的速度为327.3km/h.
点评:本题应注意审题,从题中找出光的多普勒效应并注意分析频率的变化.有些知识没有出现在课本上而是出现在阅读材料中,仔细阅读材料,从材料中找出解答问题的根据,此题有一定的拔高难度,属于难题.

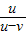 f即可.
f即可.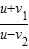 ,
,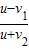 ,
,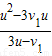 =327.3km/h.
=327.3km/h.
