
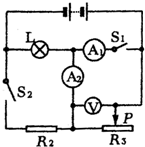
 如图所示,电灯L标有“6V 3W”字样,R2的阻值为15Ω,R3为0~30Ω的滑动变阻器,电流表A1的量程为3A,A2的量程为0.6A,电压表V的量程为3V,电源电压恒定不变.
如图所示,电灯L标有“6V 3W”字样,R2的阻值为15Ω,R3为0~30Ω的滑动变阻器,电流表A1的量程为3A,A2的量程为0.6A,电压表V的量程为3V,电源电压恒定不变. ,求滑动变阻器连入电路的阻值变化范围.
,求滑动变阻器连入电路的阻值变化范围. =
=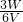 =0.5A,
=0.5A,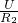 =
= =0.4A,
=0.4A, =
=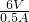 =12Ω,
=12Ω,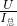 =
=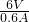 =10Ω<12Ω,
=10Ω<12Ω,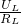 =
=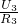 ,即
,即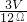 =
=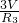 ,
, ,即PL=
,即PL= ×3W=1.92W,
×3W=1.92W, 可得,灯泡两端的最小电压:
可得,灯泡两端的最小电压: =
=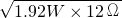 =4.8V,
=4.8V,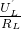 =
=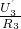 ,即
,即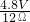 =
=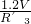 ,
, 时,滑动变阻器接入电路的电阻最小,根据P=
时,滑动变阻器接入电路的电阻最小,根据P= 求出灯泡两端的实际电压,再根据串联电路的电压特点求出滑动变阻器两端的电压,利用串联电路中的电流和欧姆定律建立等式求出滑动变阻器接入电路的最小值,进一步得出答案.
求出灯泡两端的实际电压,再根据串联电路的电压特点求出滑动变阻器两端的电压,利用串联电路中的电流和欧姆定律建立等式求出滑动变阻器接入电路的最小值,进一步得出答案.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中物理 来源: 题型:
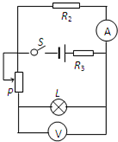 如图所示,电灯L标有“4V、1W”.滑动变阻器R总电阻为50Ω,当滑片P滑至某位置时,L恰好正常发光,此时电流表示数为0.45A,由于电路发生故障,电灯L突然熄灭,此时电流表示数变为0.5A,电压表示数变为10V,若导线完好,电路中各处接触良好,电源电压保持不变,试问:
如图所示,电灯L标有“4V、1W”.滑动变阻器R总电阻为50Ω,当滑片P滑至某位置时,L恰好正常发光,此时电流表示数为0.45A,由于电路发生故障,电灯L突然熄灭,此时电流表示数变为0.5A,电压表示数变为10V,若导线完好,电路中各处接触良好,电源电压保持不变,试问:查看答案和解析>>
科目:初中物理 来源: 题型:
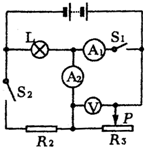 如图所示,电灯L标有“6V 3W”字样,R2的阻值为15Ω,R3为0~30Ω的滑动变阻器,电流表A1的量程为3A,A2的量程为0.6A,电压表V的量程为3V,电源电压恒定不变.
如图所示,电灯L标有“6V 3W”字样,R2的阻值为15Ω,R3为0~30Ω的滑动变阻器,电流表A1的量程为3A,A2的量程为0.6A,电压表V的量程为3V,电源电压恒定不变.| 16 | 25 |
查看答案和解析>>
科目:初中物理 来源: 题型:
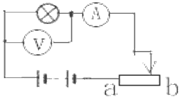 如图所示,电灯L标有“10V,5W”,滑动变阻器的最大阻值为20欧,若灯丝电阻保持不变,电源电压保持10伏不变,求滑动变阻器由a 端滑动至b 端的过程中,安培表、伏特表示数的变化范围?
如图所示,电灯L标有“10V,5W”,滑动变阻器的最大阻值为20欧,若灯丝电阻保持不变,电源电压保持10伏不变,求滑动变阻器由a 端滑动至b 端的过程中,安培表、伏特表示数的变化范围?查看答案和解析>>
科目:初中物理 来源:2010年福建省厦门一中中美班招生物理试卷(解析版) 题型:解答题
 ,求滑动变阻器连入电路的阻值变化范围.
,求滑动变阻器连入电路的阻值变化范围.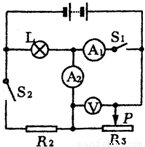
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com