
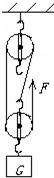
 如图所示,物体重为240N,现在拉力为100N的作用下匀速上升了2m. (不计绳重和摩擦)
如图所示,物体重为240N,现在拉力为100N的作用下匀速上升了2m. (不计绳重和摩擦) 解:(1)W有=Gh=240N×2m=480J,
解:(1)W有=Gh=240N×2m=480J, =
=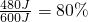 .
. (G+G动)=
(G+G动)= (240N+60N)=150N.
(240N+60N)=150N. =
=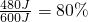 ,
, (G2+G动)=
(G2+G动)= (540N+60N)=300N.
(540N+60N)=300N. .根据物重、拉力、升高的距离能完成机械效率和动滑轮的计算.
.根据物重、拉力、升高的距离能完成机械效率和动滑轮的计算. (G+G动)计算拉力的大小.
(G+G动)计算拉力的大小. 进行有关计算.
进行有关计算.

 习题精选系列答案
习题精选系列答案科目:初中物理 来源: 题型:
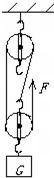 如图所示,物体重为240N,现在拉力为100N的作用下匀速上升了2m. (不计绳重和摩擦)
如图所示,物体重为240N,现在拉力为100N的作用下匀速上升了2m. (不计绳重和摩擦)查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,物体重为60N,斜面长为2m、高为1m.
如图所示,物体重为60N,斜面长为2m、高为1m.查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,物体重为100N,在水平拉力F的作用下,1秒钟内匀速前进2米,此时弹簧测力计的示数为10N(不计滑轮重及滑轮间的摩擦),则拉力F为
如图所示,物体重为100N,在水平拉力F的作用下,1秒钟内匀速前进2米,此时弹簧测力计的示数为10N(不计滑轮重及滑轮间的摩擦),则拉力F为查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,物体重为270N,现在拉力为100N的作用下匀速上升了4m.(不计摩擦和绳重)
如图所示,物体重为270N,现在拉力为100N的作用下匀速上升了4m.(不计摩擦和绳重)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com