小 托盘天平2 量筒2 ρ=

细线的粗细 这种方法不是很精确 积极鼓励表扬
分析:(1)根据题目给出的皇冠的质量是1000g和金的密度,利用V=
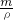
可求出1000g纯金的体积;
求出300g白银的体积加上700g金的体积即为掺了300g银的皇冠体积;
掺了白银的皇冠体积减去纯金的皇冠体积,再除以阿基米德用的桶横截面积,即为两者浸没在桶中使水面上升的高度差.
(2)掺了白银的皇冠体积减去纯金的皇冠体积,即为空心部分体积:
(3)根据疑点一计算的高度相差值(0.0319cm)来作答;
(4)要测物体的密度,首先要测质量和体积,根据题中提供的托盘天平的最大称量范围和量筒的量程来选择;
实验的关键是测出皇冠的体积,可用细线把它捆在一起浸入水中,该实验还需要的辅助器材有细线.
用排水法测体积.液体表面张力、人为因素等造成的误差,读取体积时有可能出现误差.
(5)一个定理或公式的确定,是科学家经过无数次的实验总结得出,因此对于这个《千年疑案再探》,仅凭一次实验是不能作出结论的,而且在实验中要考虑多方面要考虑多方面造成的误差,不过对小明这种勇于探索的精神应给予肯定.言之有理即可.
解答:(一)V=
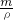
=

=51.81cm
3,
300g白银的体积为:V
1=
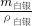
=
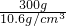
=28.30cm
3,
金的体积为V
2=
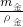
=
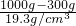
=36.27cm
3,
掺了300g银的皇冠体积为V'=V
1+V
2=28.30cm
3+36.27cm
3=64.57cm
3,
两者浸没在桶中使水面上升的高度差h=
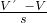
=
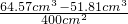
=0.0319cm.
答:1000g纯金的体积是51.81cm
3.掺了300g银的皇冠体积为64.57cm
3.两者浸没在桶中使水面上升的高度相差0.0319cm.
(二)V-V'=64.57cm
3-51.81cm
3=12.76cm
3.
答:空心部分体积是12.76cm
3.
(三)由计算的高度相差值为0.0319cm.可知高度相差值非常小
(四)要测物体的密度,首先要选择测物体的质量的仪器:托盘天平,测物体体积的仪器量筒,由皇冠的质量和体积可知,选择托盘天平2和量筒2.
实验步骤:
(1)用天平称出皇冠的质量m;
(2)将量筒内装入一定体积的水,记下水位位置的读数V
1;
(3)把皇冠用细线栓在一起,放入量筒内,让皇冠全部浸入水中,再记下水面的位置的读数V
2;
(5)皇冠的密度表达式 ρ=

=

.
故答案为:托盘天平2; 量筒2;ρ=

.
影响实验精确的因素很多,例细线要尽量细,从而减小体积测量的误差.
(五)对于小明所提出的两个疑点,他的这种方法不是很精确.不过对于小明的这种质疑精神,应积极鼓励表扬.
故答案为:这种方法不是很精确;积极鼓励表扬.
点评:此题考查了空心、混合物的密度计算,同时还考查了测量密度实验,排水法测体积是阿基米德发现的,本题重现排水法的历史渊源,并强化测固体密度的基本方法,学习中不仅要掌握测固体密度的基本方法:用天平测质量,根据排水法用量筒测密度,用ρ=

计算密度,还要掌握用数学公式、排油法、排沙法等测固体体积.是一道好题!

 细线的粗细 这种方法不是很精确 积极鼓励表扬
细线的粗细 这种方法不是很精确 积极鼓励表扬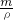 可求出1000g纯金的体积;
可求出1000g纯金的体积;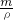 =
= =51.81cm3,
=51.81cm3,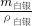 =
=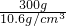 =28.30cm3,
=28.30cm3,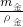 =
=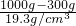 =36.27cm3,
=36.27cm3,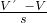 =
=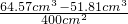 =0.0319cm.
=0.0319cm.  =
= .
. .
. 计算密度,还要掌握用数学公式、排油法、排沙法等测固体体积.是一道好题!
计算密度,还要掌握用数学公式、排油法、排沙法等测固体体积.是一道好题! 

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案