一根链条可以承受的最大拉力是7×104N,通过计算说明用这根链条能否吊起在水下体积为4m3花岗石板?如果能吊起,这块花岗石板露出水面的体积最大是多少?(不计水的阻力,ρ花岗石=2.6×103 Kg/m3,取g=10N/Kg)
解:
(1)G
石=m
石g=ρ
石v
石g=2.6×10
3kg/m
3×10N/kg×4m
3=1.04×10
5N,
∵石块在水中,v
排=v
石=4m
3,
∴石块在水中受浮力:
F
浮=ρ
水gv
排=v
石=1×10
3kg/m
3×10N/kg×4m
3=4×10
4N,
∵F
浮+F
拉=4×10
4N+7×10
4N=1.1×10
5N>1.04×10
5N,
∴能将石块从水中提起.
(2)当最大拉力F
大=7×10
4N时,
F′
浮=G-F
大=1.04×10
5N-7×10
4N=3.4×10
4N,
∵F
浮=ρ
水gv
排,
∴石块排开水面的最大体积:
v′
排=
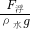
=
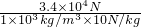
=3.4m
3,
石块露出水面的最大体积:
V
露=V-V
排′=4m
3-3.4m
3=0.6m
3.
答:能将这块花岗石板从水中提起,花岗石板露出水面体积最大为0.6m
3.
分析:(1)在水中,石块受到竖直向下的重力、竖直向上的浮力和拉力,若重力小于浮力与拉力的和,石块能被拉起,否则不能被拉起;
(2)当拉力为1×10
4N时,求出这块花岗石板所受的浮力,根据阿基米德原理求出这块花岗石板排开水面的最大体积,知道花岗石的体积,可求花岗石露出水面的最大体积.
点评:本题考查了学生对阿基米德原理变形公式的掌握和运用,涉及到同一直线反方向的力的合成,属于难题.

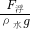 =
=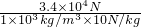 =3.4m3,
=3.4m3,
