Question

小芳家里新买了一台电热水器，从“用户手册”中，她获得了以下资料，请根据这些资料完成相应的计算：
（一）、外形尺寸（mm）

A	B	C	D	E	F
781	100	196	196	353	434

（二）、技术数据

额定功率/W	1000/1500/2500	额定电压/Mpa	0.8
额定电压/V	交流 220	容积/L	50
频率/Hz	50	净重/kg	19

（1）如图为安装示意图，安装时要将L形挂钩用膨胀螺钉固定在承重墙上，上表是热水器的部分数据，请估算L形挂钩受到的最大向下拉力F及对应此时膨胀螺钉与承重墙体间的摩擦力f．
（2）这台热水器共有三挡加热功率，销售人员曾介绍说：热水器内部有两个加热管．请你根据销售人员的介绍，猜测并画出内部加热电路的主要结构（简化的等效电路图）．然后依据你的猜想，计算出每个加热管的电阻值．
（3）产品说明书上标明：当达到设定温度，停止加热后，如果水温降到低于设定温度4℃时，热水器将自动以设置功率将桶内的水加热至设定温度，如此反复直至手动停止加热．小芳想到了国家提倡的峰谷电价制度的有关规定：2011年起，本地的分时电价为：峰时段（08：00～22：00）0.6元/度，谷时段（22：00～次日08：00）0.3元/度．她想，如果每天下午6点洗浴时需要把20℃的冷水加热至50℃，可以下午直接加热，也可以早晨8点前加热好，让热水器自动保温至下午6点，哪种方式更省钱呢？为此她利用热水器提供的测温功能测量了水温从50℃降至46℃需要190分钟，已知c_水=4.2×10³J/（kg?℃），请帮她通过计算做出哪种方式更省钱的判断．

Answer 1

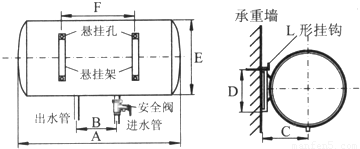
分析：（1）用铭牌可知电热水器的净重和容积，根据m=ρV和G=mg求出电热水器的总重，然后对静止的热水器受力分析，根据二力平衡条件可知竖直方向对L形挂钩向下的拉力；以悬挂架下端为轴，可以把热水器看成杠杆，根据杠杆的平衡条件求出电热水器上端所受的水平向左的拉力即膨胀螺钉所受的摩擦力．
（2）这台热水器共有三挡加热功率且最大功率等于剩余两功率之和据此可以猜想两电热管并联，据此画出等效电路图；根据R=

U2

P

分别求出两加热管的电阻．
（3）忽略加热过程的热损失，根据W=Q=cm△t求出直接加热消耗的电能，并求出下午加热支出的电费；先求出早晨8点前加热支出的电费，再根据W=Q=cm△t求出加热升温4℃所需电能和最大功率加热时的时间，因时间很小可以忽略不计；降低4℃所需时间为190min，至下午6点共需要三次加热，进一步求出三次消耗的电能和支出的电费，总电费等于这两者之和；然后比较这中方案支出的电费即可判断那种更经济．

解答：解：（1）电热水器的总重：
G_总=m_电g+ρ_水gV=19×10N/kg+1.0×10³kg/m³×50×10^-3m³×10N/kg=690N，
电热水器挂在L形挂钩上时，其受力情况如下：

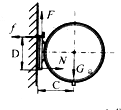
挂钩竖直方向：向上的拉力F和向下电热水器的总重G_总，
水平方向：向右的支持力和向左膨胀螺钉的拉力，此时膨胀螺钉受到的拉力和摩擦力是一对平衡力；
因电热水器静止，所以沿竖直方向二力平衡，因此对L形挂钩向下的拉力
F=G=690N；
因L形挂钩静止，电热水器上端所受的水平向左的拉力等于膨胀螺钉所受的摩擦力；
以悬挂架下端为轴，把热水器看成杠杆，则根据杠杆的平衡条件可得fD=G_总C，
f=

G总C

D

=

690N×196mm

196mm

=690N．
（2）由热水器的三档位的数值关系猜测得热水器加热部分的等效电路图如下图所示：

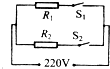
其中加热管R₁的额定功率为1000W，电热管R₂的额定功率为1500W；
加热管的电阻分别为：
R₁=

U2

P1

=

(220V)2

1000W

=48.4Ω，
R₂=

U2

P2

=

(220V)2

1500W

≈32.3Ω．
（3）①忽略加热过程的热损失，直接加热消耗的电能为：
W₁=Q₁=cm△t₁=4.2×10³J/（kg?℃）×50kg×（50℃-20℃）=6.3×10⁶J=1.75KW?h，
下午加热的电费支出为：
0.6元/KW?h×1.75KW?h=1.05元；
②早晨8点前加热，电费支出为：
0.3元/KW?h×1.75KW?h=0.525元；
加热升温4℃所需电能：
W₂=Q₂=cm△t₂=4.2×10³J/（kg?℃）×50kg×（50℃-46℃）=8.4×10⁵J，
加热升温4℃所需时间（设加热功率为2500W）
t₁=

W2

P3

=

8.4×105J

2500W

=336s=5.6min，（这段加热时间可以忽略不计）
降低4℃所需时间为190min，至下午6点共需要三次加热，消耗电能：
W₃=3W₂=3×8.4×10⁵J=2.52×10⁶J=0.7KW?h，
电费支出：
0.6元/KW?h×0.7KW?h=0.42元；
总支出：
0.525元+0.42元=0.945元，
所以，第二方案更省钱．
答：（1）L形挂钩受到的最大向下拉力为690N，此时膨胀螺钉与承重墙体间的摩擦力为690N．
（2）内部加热电路的主要结构如上图所示，每个加热管的电阻值分别为48.4Ω、32.3Ω．
（3）第二方案更省钱．

点评：本题考查了密度公式、重力公式、电功公式、二力平衡条件和杠杆平衡条件的应用，关键是公式和规律的灵活运用，难点是对L形支架正确的受力分析和根据档位画出等效电路图以及明确两种加热方案中消耗电能的计算．