
 在图所示的装置中,质量可忽略不计的杠杆CD可绕转轴O点自由转动,OC:OD=2:1,A、B两个滑轮的质量均为2kg,E是边长为20cm、密度为ρ1的正方体合金块,合金块E通过滑轮A用轻细线悬吊着全部浸没在密度为ρ2的液体中.当质量为60kg的人用F1=75N的力竖直向下拉绳时,杠杆恰好在水平位置平衡,此时人对地面的压强为p1=1.05×104Pa;若把密度为ρ2的液体换成密度为ρ3的液体,合金块E全部浸没在密度为ρ3的液体中,人用F2的力竖直向下拉绳,杠杆在水平位置平衡,此时人对地面的压强为p2=1.034×104Pa.若ρ2:ρ3=5:4,取g=10N/kg,人与地面接触的面积保持不变,杠杆和滑轮的摩擦均可忽略不计,求:
在图所示的装置中,质量可忽略不计的杠杆CD可绕转轴O点自由转动,OC:OD=2:1,A、B两个滑轮的质量均为2kg,E是边长为20cm、密度为ρ1的正方体合金块,合金块E通过滑轮A用轻细线悬吊着全部浸没在密度为ρ2的液体中.当质量为60kg的人用F1=75N的力竖直向下拉绳时,杠杆恰好在水平位置平衡,此时人对地面的压强为p1=1.05×104Pa;若把密度为ρ2的液体换成密度为ρ3的液体,合金块E全部浸没在密度为ρ3的液体中,人用F2的力竖直向下拉绳,杠杆在水平位置平衡,此时人对地面的压强为p2=1.034×104Pa.若ρ2:ρ3=5:4,取g=10N/kg,人与地面接触的面积保持不变,杠杆和滑轮的摩擦均可忽略不计,求: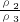 =
=
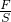 ,
,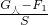 =
=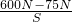 =
=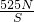 =1.05×104Pa,
=1.05×104Pa,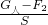 ,
,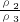 =
= ③,
③,

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中物理 来源: 题型:
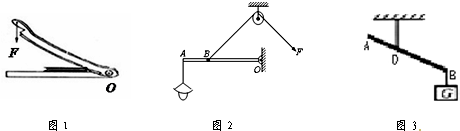
 (2010?宣武区二模)如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求:
(2010?宣武区二模)如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求:查看答案和解析>>
科目:初中物理 来源: 题型:
 (2012?丹东)某剧组为拍摄需要,设计了如图所示的装置来改变照明灯的高度.轻质杠杆ABO可绕O点转动,在图中画出ABO所受阻力F2的示意图,并画出动力臂L1和阻力臂L2.
(2012?丹东)某剧组为拍摄需要,设计了如图所示的装置来改变照明灯的高度.轻质杠杆ABO可绕O点转动,在图中画出ABO所受阻力F2的示意图,并画出动力臂L1和阻力臂L2.查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 过去几百年来许多人一直致力于发明一种永动机,包括伟大的科学家牛顿,但都以失败告终.近几年来,科学家发现某种合金具有“形状记忆功能”:如果在较低温度时将它弯曲成某一形状,然后加热到较高温度时再弯曲成另一形状,那么当降低到原来较低温度时,它就会自行恢复到低温时的形状.现用它制成如图所示的装置:在可绕圆心O转动的均匀轻质圆盘上,安装一个用形状记忆合金做成的螺旋圈,它们在温度低时收紧、温度高时放松.实验表明:当把该圆盘的下半部分浸在盛有一定量热水的水槽中时,只要给圆盘一个起始转动的力,圆盘就能克服摩擦和水的阻力连续转动起来.这不就是一个可以不消耗能量的“永动机”吗?
过去几百年来许多人一直致力于发明一种永动机,包括伟大的科学家牛顿,但都以失败告终.近几年来,科学家发现某种合金具有“形状记忆功能”:如果在较低温度时将它弯曲成某一形状,然后加热到较高温度时再弯曲成另一形状,那么当降低到原来较低温度时,它就会自行恢复到低温时的形状.现用它制成如图所示的装置:在可绕圆心O转动的均匀轻质圆盘上,安装一个用形状记忆合金做成的螺旋圈,它们在温度低时收紧、温度高时放松.实验表明:当把该圆盘的下半部分浸在盛有一定量热水的水槽中时,只要给圆盘一个起始转动的力,圆盘就能克服摩擦和水的阻力连续转动起来.这不就是一个可以不消耗能量的“永动机”吗?查看答案和解析>>
科目:初中物理 来源: 题型:
 小丽同学利用如图所示的装置,将系在细线上的轻质小球靠近音叉来探究“声音的强弱与什么因素有关”.实验中通过改变施力的大小来改变声源的振幅.
小丽同学利用如图所示的装置,将系在细线上的轻质小球靠近音叉来探究“声音的强弱与什么因素有关”.实验中通过改变施力的大小来改变声源的振幅.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com