
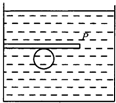
 如图所示,圆柱形容器中盛有某种液体,在它的侧壁上固定了一块水平挡板,下方有一个体积为103 cm3、质量为500g的实心小球被挡住,液体深为50cm,对容器底的压强为4.0×103Pa.(取g=10N/kg)求:
如图所示,圆柱形容器中盛有某种液体,在它的侧壁上固定了一块水平挡板,下方有一个体积为103 cm3、质量为500g的实心小球被挡住,液体深为50cm,对容器底的压强为4.0×103Pa.(取g=10N/kg)求: =
=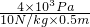 =0.8×103kg/m3.
=0.8×103kg/m3.

科目:初中物理 来源: 题型:
 (2012?鄂州模拟)如图所示,圆柱形容器中盛有某种液体,在它的侧壁上固定了一块水平挡板,下方有一个体积为103 cm3、质量为500g的实心小球被挡住,液体深为50cm,对容器底的压强为4.0×103Pa.(取g=10N/kg)求:
(2012?鄂州模拟)如图所示,圆柱形容器中盛有某种液体,在它的侧壁上固定了一块水平挡板,下方有一个体积为103 cm3、质量为500g的实心小球被挡住,液体深为50cm,对容器底的压强为4.0×103Pa.(取g=10N/kg)求:查看答案和解析>>
科目:初中物理 来源: 题型:
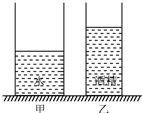 (2013?松江区三模)如图所示,圆柱形容器甲和乙放在水平桌面上,它们的底面积分别为0.02米2和0.01米2.容器甲中盛有0.2米高的水,容器乙中盛有0.3米高的酒精.
(2013?松江区三模)如图所示,圆柱形容器甲和乙放在水平桌面上,它们的底面积分别为0.02米2和0.01米2.容器甲中盛有0.2米高的水,容器乙中盛有0.3米高的酒精.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2011?顺义区二模)如图所示的圆柱形容器里盛有0.8kg某种液体,容器的底面积为0.01m2、高为0.15m;图中A点在B点的正上方,两点间的距离为O.02m,两点间液体压强的差值为160Pa.现往容器里放入一物块,结果液面恰好与容器口相平(没有液体溢出),物块漂浮,则下列说法正确的有( )(g=10N/kg)
(2011?顺义区二模)如图所示的圆柱形容器里盛有0.8kg某种液体,容器的底面积为0.01m2、高为0.15m;图中A点在B点的正上方,两点间的距离为O.02m,两点间液体压强的差值为160Pa.现往容器里放入一物块,结果液面恰好与容器口相平(没有液体溢出),物块漂浮,则下列说法正确的有( )(g=10N/kg)查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,圆柱形容器的横截面积为S,盛有适量的水,放入木块A,静止后水面上升了h1;在A下方挂上物块B,静止后水面又上升了h2,且水面恰好到达容器口.下列说法错误的是( )
如图所示,圆柱形容器的横截面积为S,盛有适量的水,放入木块A,静止后水面上升了h1;在A下方挂上物块B,静止后水面又上升了h2,且水面恰好到达容器口.下列说法错误的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com