
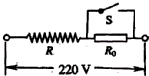
 电热毯是农村普遍采用的取暖工具,小明使用的是一个两档(一档是100W,另一档是25W)的电热毯.电热毯电路如图所示,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.
电热毯是农村普遍采用的取暖工具,小明使用的是一个两档(一档是100W,另一档是25W)的电热毯.电热毯电路如图所示,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.
 可得:
可得: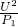 =
=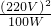 =484Ω,
=484Ω, =
= =(
=(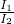 )2=
)2=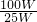 =
=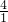 ,
,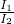 =
= ,
,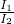 =
=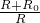 =
= ,
, 求出R的阻值;断开开关S时,R与R0串联,根据P=I2R分别表示出两种情况下R的电功率即可求出两电流关系,利用电阻的串联和欧姆定律表示出电源的电压,利用电源的电压不变即可求出R与R0的阻值关系,进一步求出R0的阻值;
求出R的阻值;断开开关S时,R与R0串联,根据P=I2R分别表示出两种情况下R的电功率即可求出两电流关系,利用电阻的串联和欧姆定律表示出电源的电压,利用电源的电压不变即可求出R与R0的阻值关系,进一步求出R0的阻值;

科目:初中物理 来源: 题型:
 (2007?丰台区二模)电热毯是农村普遍采用的取暖工具,小明使用的是一个两档(一档是100W,另一档是25W)的电热毯.电热毯电路如图所示,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.
(2007?丰台区二模)电热毯是农村普遍采用的取暖工具,小明使用的是一个两档(一档是100W,另一档是25W)的电热毯.电热毯电路如图所示,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2005?烟台)电热毯是农村普遍采用的取暖工具,小明使用的是一床两档(一档是100W,另一档是25W)电热毯.观察电热毯外部结构,小明猜想,电热毯是由电热丝和一个开关组成,开关盒内可能有一个定值电阻R.电热毯的电路如图,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.从能源有效利用的角度,计算说明小明的猜想不是十分合理.
(2005?烟台)电热毯是农村普遍采用的取暖工具,小明使用的是一床两档(一档是100W,另一档是25W)电热毯.观察电热毯外部结构,小明猜想,电热毯是由电热丝和一个开关组成,开关盒内可能有一个定值电阻R.电热毯的电路如图,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.从能源有效利用的角度,计算说明小明的猜想不是十分合理.查看答案和解析>>
科目:初中物理 来源: 题型:
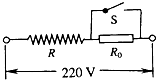 (2006?河西区二模)电热毯是农村普遍采用的取暖工具,小明使用的是一床两档(一档是100W,另一档是25W)的电热毯.观察电热毯外部结构,小明猜想:电热毯是由电热丝和一个开关组成,开关盒内可能有一个定值电阻R0,电热毯电路如图所示,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W,若电热毯的实际电路如图所示:
(2006?河西区二模)电热毯是农村普遍采用的取暖工具,小明使用的是一床两档(一档是100W,另一档是25W)的电热毯.观察电热毯外部结构,小明猜想:电热毯是由电热丝和一个开关组成,开关盒内可能有一个定值电阻R0,电热毯电路如图所示,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W,若电热毯的实际电路如图所示:查看答案和解析>>
科目:初中物理 来源:天津模拟题 题型:计算题
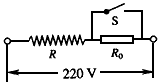
查看答案和解析>>
科目:初中物理 来源:2005年山东省烟台市中考物理试卷(解析版) 题型:解答题
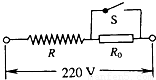 电热毯是农村普遍采用的取暖工具,小明使用的是一床两档(一档是100W,另一档是25W)电热毯.观察电热毯外部结构,小明猜想,电热毯是由电热丝和一个开关组成,开关盒内可能有一个定值电阻R.电热毯的电路如图,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.从能源有效利用的角度,计算说明小明的猜想不是十分合理.
电热毯是农村普遍采用的取暖工具,小明使用的是一床两档(一档是100W,另一档是25W)电热毯.观察电热毯外部结构,小明猜想,电热毯是由电热丝和一个开关组成,开关盒内可能有一个定值电阻R.电热毯的电路如图,闭合开关S时,电热丝发热功率为100W,断开开关S时,电热丝发热功率为25W.从能源有效利用的角度,计算说明小明的猜想不是十分合理.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com