
 有一根细木棒,在A处挂一吹足空气的气球,在O处用一根细绳将细木棒悬挂起来,这时,细木棒恰能保持水平,如图所示.现用一钢针在气球水平直径的两端各刺一个小洞,使球中的空气逐步缓慢泄出,气球体积同时逐渐减小.对这一过程中细木棒位置变化的判断及其原因分析最正确、全面的是
有一根细木棒,在A处挂一吹足空气的气球,在O处用一根细绳将细木棒悬挂起来,这时,细木棒恰能保持水平,如图所示.现用一钢针在气球水平直径的两端各刺一个小洞,使球中的空气逐步缓慢泄出,气球体积同时逐渐减小.对这一过程中细木棒位置变化的判断及其原因分析最正确、全面的是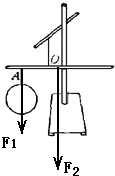 密度也减小,
密度也减小,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中物理 来源: 题型:
 有一根细木棒,在A处挂一吹足空气的气球,在O处用一根细绳将细木棒悬挂起来,这时,细木棒恰能保持水平,如图所示.现用一钢针在气球水平直径的两端各刺一个小洞,使球中的空气逐步缓慢泄出,气球体积同时逐渐减小.对这一过程中细木棒位置变化的判断及其原因分析最正确、全面的是( )
有一根细木棒,在A处挂一吹足空气的气球,在O处用一根细绳将细木棒悬挂起来,这时,细木棒恰能保持水平,如图所示.现用一钢针在气球水平直径的两端各刺一个小洞,使球中的空气逐步缓慢泄出,气球体积同时逐渐减小.对这一过程中细木棒位置变化的判断及其原因分析最正确、全面的是( )查看答案和解析>>
科目:初中物理 来源:2008-2009学年四川省资阳市雁江区九年级(上)期中物理联考试卷(解析版) 题型:选择题

查看答案和解析>>
科目:初中物理 来源:1992年上海市第六届初中物理竞赛复赛试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com