

分析 (1)由定值电阻的规格可知允许通过的最大电流,根据P=I2R求出R0上允许消耗的最大功率;
(2)由图乙可知,电子元件的阻值R与压力F的关系为一次函数,设出表达式,从图象中读出两组数据代入得出表达式;
(3)根据滑动变阻器允许通过的最大电流可知电路中的最大电流,根据欧姆定律求出电路中的总电阻,利用电阻的串联求出R的阻值,然后代入电子元件的阻值R随压力F变化的关系式求出该测力计所能测量的最大压力;
(4)由R随压力F变化的关系式,若要增大该测力计的量程,应从如何减小R的电阻值上分析解答.
解答 解:(1)定值电阻R0的规格可知,电阻R0允许通过的最大电流I0=0.01A,
则R0允许消耗的最大功率:
P0=I02R0=(0.01A)2×520Ω=0.052W;
(2)由图乙可知,电子元件的阻值R与压力F的关系为一次函数,设为R=kF+b,
由图象可知,当F=0时R=200Ω,当F=50N时R=180Ω,则
200Ω=k×0N+b,180Ω=k×50N+b,
联立等式可得:b=200Ω,k=-0.4Ω/N,
电子元件的阻值R随压力F变化的关系式R=-0.4Ω/N×F+200Ω;
(3)电路中的最大电流I0=0.01A,由I=$\frac{U}{R}$可得,电路中的总电阻:
R总=$\frac{U}{{I}_{0}}$=$\frac{6V}{0.01A}$=600Ω,
因串联电路中总电阻等于各分电阻之和,
所以,R的最小阻值:
R=R总-R0=600Ω-520Ω=80Ω,
此时R上的压力最大,则
80Ω=-0.4Ω/N×F+200Ω,
解得F=300N;
(4)要增大该测力计的量程,由F=$\frac{200Ω-R}{0.4Ω/N}$知,应减小R值,
电路中的电压一定时,最大电流也一定,总电阻不变,可以增大R0的阻值从而减小R的阻值;
电流一定时,也可以减小总电阻,从而减小R值,可以减小电源的电压从而减小电路中的总电阻.
答:(1)R0允许消耗的最大功率是0.052W;
(2)电子元件的阻值R随压力F变化的关系式为R=-0.4Ω/N×F+200Ω;
(3)该测力计所能测量的最大压力是300N;
(4)若要增大该测力计的量程,可以增大R0的阻值,也可以减小电源的电压.
点评 本题考查了电路的动态分析与计算以及串联电路特点和欧姆定律的应用,关键是用好R随压力F变化的关系式.


 优学名师名题系列答案
优学名师名题系列答案科目:初中物理 来源: 题型:选择题
| A. | 总电阻 | B. | 总电流 | C. | 总功率 | D. | 无法判断 |
查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 如图所示为“无人机”(多功能飞行器),它具有4个旋翼,可通过无线电进行操控,其在拍摄调查、无人配送等方面具有广阔的前景.
如图所示为“无人机”(多功能飞行器),它具有4个旋翼,可通过无线电进行操控,其在拍摄调查、无人配送等方面具有广阔的前景.查看答案和解析>>
科目:初中物理 来源: 题型:选择题
| A. | ①和② | B. | ②和③ | C. | ①和④ | D. | ②和④ |
查看答案和解析>>
科目:初中物理 来源: 题型:解答题
| (1)我们知道,原子有原子核和核外电子组成,核外电子绕原子核高速旋转.按照波尔理论,电子绕原子核做匀速圆周运动,且电子会受到原子核的静电吸引力(如图甲).已知,电子受到的静电吸引力F电与原子序数Z成正比,与元电荷e的平方成正比,与电子运动的轨道半径r的平方的关系如右图乙图象所示,k是静电常数.则电子所受的静电吸引力的数学表达式为:B. A.${F_电}=\frac{{Z{e^2}{r^2}}}{4πk}$B.${F_电}=\frac{{Z{e^2}}}{{4πk{r^2}}}$C.${F_电}=\frac{e^2}{{4πkZ{r^2}}}$D.${F_电}=\frac{{Z{r^2}}}{{4πk{e^2}}}$ 其中静电常数k=8.85×10-12,当物体做匀速圆周运动时,必须受到一个向圆心拉的力,这个力叫做向心力,电子绕原子核做匀速圆周运动的向心力${F_心}=m\frac{υ^2}{r}$,其中m为电子的质量,υ为电子的运动速度.且电子做圆周运动的向心力等于电子受到的静电吸引力. (2)波尔引用量子理论,提出电子运动的轨道不是任意的,轨道数n从内向外依次为1、2、3、…,(如图丙)并且提出$mυr=n\frac{h}{2π}$,其中n为轨道数,h为常数,h=6.63×10-34J•s.请推导出电子的轨道速度υ的数学表达式. (3)已知氧原子的原子序数Z=8,元电荷e=1.6×10-19C,求氧原子中电子在轨道数n=2的轨道上运动式的速度υ2= 8.73×106m/s. | 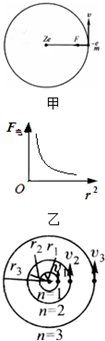 |
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:解答题
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com