
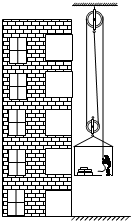
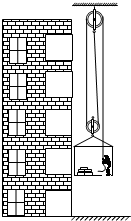
 在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求:
在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求: (G人+G砖1+G架+G动)=
(G人+G砖1+G架+G动)= (1750N+G动)
(1750N+G动) (1750N+G动)
(1750N+G动) (G人+G砖2+G架+G动)=
(G人+G砖2+G架+G动)= (2050N+G动)
(2050N+G动) (2050N+G动)
(2050N+G动) (1750N+G动)]:[850N-
(1750N+G动)]:[850N- (2050N+G动)]=5:3
(2050N+G动)]=5:3 =
= =5kg,
=5kg,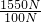 =15.5块≈15块,
=15.5块≈15块, (G人+G砖′+G架+G动)=
(G人+G砖′+G架+G动)= (850N+1500N+100N+50N)=
(850N+1500N+100N+50N)=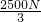 ,
, =
=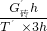 =
= =60%.
=60%. (G人+G砖1+G架+G动)求出绳子的拉力,人对框架底的压力等于人的重力减掉绳子的拉力,同理提升11块地板砖时人对绳的拉力,然后利用F1:F2=5:3得出等式,即可求出动滑轮的重力,最后利用G=mg求出动滑轮的质量;
(G人+G砖1+G架+G动)求出绳子的拉力,人对框架底的压力等于人的重力减掉绳子的拉力,同理提升11块地板砖时人对绳的拉力,然后利用F1:F2=5:3得出等式,即可求出动滑轮的重力,最后利用G=mg求出动滑轮的质量; =
=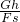 =
=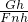 =
=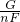 计算.
计算.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中物理 来源: 题型:
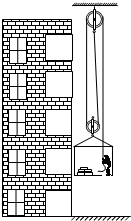 在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求:
在装修房屋时,一个质量为85kg的人,用图所示的装置(包括滑轮组及装货物的框架)提升地板砖运到房间中.已知装货物的框架重100N,每块地板砖重100N,滑轮与轴的摩擦和绳重均忽略不计,当提升8块地板砖时,人对框架底的压力为F1;当提升11块地板砖时人对框架底的压力为F2,且F1:F2=5:3.(取g=10N/kg)求:查看答案和解析>>
科目:初中物理 来源:不详 题型:问答题
查看答案和解析>>
科目:初中物理 来源:2011-2012学年上海市黄浦区光明初中九年级(上)期中物理练习试卷(解析版) 题型:解答题
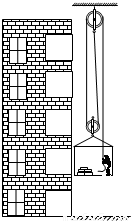
查看答案和解析>>
科目:初中物理 来源:009-2010学年北京市海淀区九年级(上)期中物理试卷(解析版) 题型:解答题
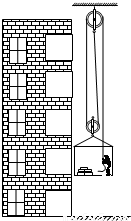
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com