
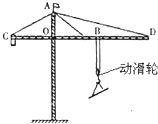
 “塔吊”是建筑工地上普遍使用的起重设备.如图所示的“塔吊”用到的简单机械有:________,用此“塔吊”将0.8t的钢材竖直匀速吊起8m高,钢绳的拉力为5000N,则滑轮组的机械效率是________.若用此“塔吊”将1t的钢材匀速提高1m,滑轮组做________J的功.(不计摩擦和钢绳的重力)
“塔吊”是建筑工地上普遍使用的起重设备.如图所示的“塔吊”用到的简单机械有:________,用此“塔吊”将0.8t的钢材竖直匀速吊起8m高,钢绳的拉力为5000N,则滑轮组的机械效率是________.若用此“塔吊”将1t的钢材匀速提高1m,滑轮组做________J的功.(不计摩擦和钢绳的重力) 求出机械效率.
求出机械效率. (G+G动)求出动滑轮重,再根据F=
(G+G动)求出动滑轮重,再根据F= (G+G动)求出第二次的拉力,根据s=2h求出拉力移动距离,根据W=Fs求出滑轮组做的功.
(G+G动)求出第二次的拉力,根据s=2h求出拉力移动距离,根据W=Fs求出滑轮组做的功. ×100%=
×100%= ×100%=78.4%;
×100%=78.4%; (G+G动)
(G+G动) (G′+G动)=
(G′+G动)= ×(9800N+2160N)=5980N,
×(9800N+2160N)=5980N, (G+G动)是解决此题的关键.
(G+G动)是解决此题的关键. 

科目:初中物理 来源: 题型:
 40、“塔吊”是建筑工地上普遍使用的起重设备.如图所示的“塔吊”,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦不计.
40、“塔吊”是建筑工地上普遍使用的起重设备.如图所示的“塔吊”,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦不计.查看答案和解析>>
科目:初中物理 来源: 题型:
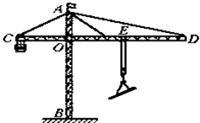 “塔吊”是建筑工地上普遍使用的起重设备.如图20中的“塔吊”,AB是竖直支架,CD是水平臂,期上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦忽略不计.OE=15m时,若用此“塔吊”能起吊重物的最大物重是8000N,求配重体有多重?当滑轮组移到D点(OD=25m)时能够安全起吊重物的最大重量是多少?(OC=10m)
“塔吊”是建筑工地上普遍使用的起重设备.如图20中的“塔吊”,AB是竖直支架,CD是水平臂,期上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦忽略不计.OE=15m时,若用此“塔吊”能起吊重物的最大物重是8000N,求配重体有多重?当滑轮组移到D点(OD=25m)时能够安全起吊重物的最大重量是多少?(OC=10m)查看答案和解析>>
科目:初中物理 来源: 题型:
 (2011?泸州)“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在)O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1.5×103Kg,则配重体的质量应为
(2011?泸州)“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在)O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1.5×103Kg,则配重体的质量应为查看答案和解析>>
科目:初中物理 来源: 题型:
 “塔吊”是建筑工地上普遍使用的起重设备. 如图中的“塔吊”将8000N的钢材先竖直匀速向上吊起8m,在此上升过程中,塔吊对钢材所做的功W1=
“塔吊”是建筑工地上普遍使用的起重设备. 如图中的“塔吊”将8000N的钢材先竖直匀速向上吊起8m,在此上升过程中,塔吊对钢材所做的功W1=查看答案和解析>>
科目:初中物理 来源: 题型:
 “塔吊”是建筑工地上普遍使用的一种起重设备,如图是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,(不计“水平臂”和滑轮重力)
“塔吊”是建筑工地上普遍使用的一种起重设备,如图是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,(不计“水平臂”和滑轮重力)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com