
 如图所示电路,设电源电压不变,灯丝电阻不随温度变化,滑动变阻器的最大阻值为R.当开关S1、S2断开,滑动变阻器的滑片P位于A端时,电压表V2示数为U2,电阻R2和滑动变阻器消耗的总功率为P1=2.4W;当开关S1断开,S2闭合时,电压表V1示数为U1,灯正常发光,电流表的示数为I;当开关S1、S2都闭合时,接入电路的滑动变阻器阻值为最大值的2/3时,电流表的示数与I相比变化了△I=1.4A,滑动变阻器消耗的电功率为P2=14.7W.已知U1:U2=7:6.求:
如图所示电路,设电源电压不变,灯丝电阻不随温度变化,滑动变阻器的最大阻值为R.当开关S1、S2断开,滑动变阻器的滑片P位于A端时,电压表V2示数为U2,电阻R2和滑动变阻器消耗的总功率为P1=2.4W;当开关S1断开,S2闭合时,电压表V1示数为U1,灯正常发光,电流表的示数为I;当开关S1、S2都闭合时,接入电路的滑动变阻器阻值为最大值的2/3时,电流表的示数与I相比变化了△I=1.4A,滑动变阻器消耗的电功率为P2=14.7W.已知U1:U2=7:6.求: 时,等效电路图如图丙所示;
时,等效电路图如图丙所示;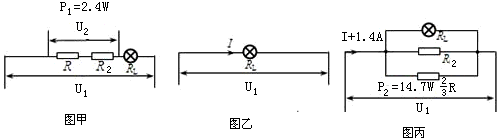
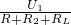 )2×(R+R2),
)2×(R+R2),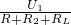 )2×(R+R2)----------①
)2×(R+R2)----------①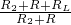 =
= ,
,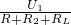 )2×(R+R2)=(
)2×(R+R2)=(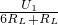 )2×6RL
)2×6RL +
+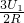 ,
, +
+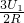 ---------③
---------③ ,
,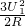 =14.7W--------------④
=14.7W--------------④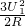 =
=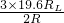 ,
, +
+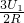 =
=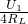 +
+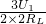 =
= ,
, =1.4A;
=1.4A; 可知,滑动变阻器的阻值最大时,电路消耗的电功率最小;
可知,滑动变阻器的阻值最大时,电路消耗的电功率最小;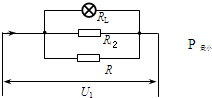
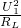 +
+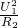 +
+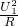 =
=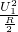 +
+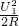 +
+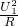 =
= ×
×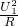 ,
,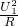 =9.8W,
=9.8W, ×9.8W=34.3W.
×9.8W=34.3W. 表示出此时滑动变阻器消耗的电功率;联立以上方程得出三电阻之间的关系,以及U1和RL之间的关系,即可求出灯正常发光时通过灯L的电流.
表示出此时滑动变阻器消耗的电功率;联立以上方程得出三电阻之间的关系,以及U1和RL之间的关系,即可求出灯正常发光时通过灯L的电流. 可知,滑动变阻器的阻值最大时,电路消耗的电功率最小;利用P=
可知,滑动变阻器的阻值最大时,电路消耗的电功率最小;利用P= 分别表示出其大小,再根据三电阻之间的关系和图丙中滑动变阻器消耗的电功率即可求出电路消耗的最小总功率.
分别表示出其大小,再根据三电阻之间的关系和图丙中滑动变阻器消耗的电功率即可求出电路消耗的最小总功率.

科目:初中物理 来源: 题型:
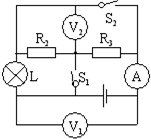 (2009?石景山区一模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化.当只闭合开关S1时,电流表的示数是I1.当只闭合开关S2时,电流表的示数是I2.当断开S1、S2时,电流表的示数是I3,电压表V1、V2示数之比为2:1,此时RL消耗的电功率为0.24W;当开关S1、S2闭合时,灯L正常发光,电流表的示数为I4.已知I1:I2=2:1,(电路图中所有的交叉点都相连)求:
(2009?石景山区一模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化.当只闭合开关S1时,电流表的示数是I1.当只闭合开关S2时,电流表的示数是I2.当断开S1、S2时,电流表的示数是I3,电压表V1、V2示数之比为2:1,此时RL消耗的电功率为0.24W;当开关S1、S2闭合时,灯L正常发光,电流表的示数为I4.已知I1:I2=2:1,(电路图中所有的交叉点都相连)求:查看答案和解析>>
科目:初中物理 来源: 题型:
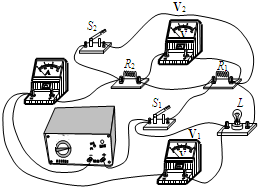 (2013?东城区一模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化.当只闭合开关S1时,电流表的示数是I1.当只闭合开关S2时,电流表的示数是I2.当开关S1、S2都闭合时,灯L正常发光,电流表的示数为I3.当开关S1、S2都断开时,电流表的示数是I4,电压表V1、V2示数之比为3:1,此时RL消耗的电功率为0.5W;已知I1:I2=3:1,求:
(2013?东城区一模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化.当只闭合开关S1时,电流表的示数是I1.当只闭合开关S2时,电流表的示数是I2.当开关S1、S2都闭合时,灯L正常发光,电流表的示数为I3.当开关S1、S2都断开时,电流表的示数是I4,电压表V1、V2示数之比为3:1,此时RL消耗的电功率为0.5W;已知I1:I2=3:1,求:查看答案和解析>>
科目:初中物理 来源: 题型:
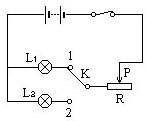 如图所示电路,设电源电压恒定,滑动变阻器的最大阻值为16欧,灯L1标有“6V 3W”,灯L2标有“6V 6W”,灯丝电阻不随温度变化.当开关K在接点1位置时,滑动变阻器滑片P位于中点,灯L1正常发光;当开关K由接点1转到接点2时,适当调节滑片P的位置,使灯L2也能正常发光.
如图所示电路,设电源电压恒定,滑动变阻器的最大阻值为16欧,灯L1标有“6V 3W”,灯L2标有“6V 6W”,灯丝电阻不随温度变化.当开关K在接点1位置时,滑动变阻器滑片P位于中点,灯L1正常发光;当开关K由接点1转到接点2时,适当调节滑片P的位置,使灯L2也能正常发光.查看答案和解析>>
科目:初中物理 来源: 题型:
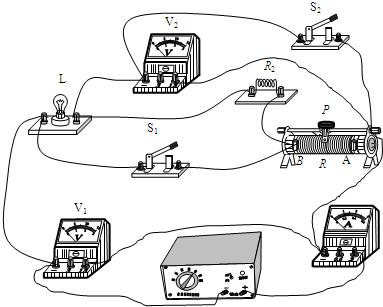 (2011?北京二模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化,滑动变阻器的最大阻值为R.当开关S1、S2断开,滑动变阻器的滑片P位于A端时,电压表V2示数为U2,电阻R2和滑动变阻器消耗的总功率为P1=2.4W;当开关S1断开,S2闭合时,电压表V1示数为U1,灯正常发光,电流表的示数为I;当开关S1、S2都闭合时,接入电路的滑动变阻器阻值为最大值的2/3时,电流表的示数与I相比变化了△I=1.4A,滑动变阻器消耗的电功率为P2=14.7W.已知U1:U2=7:6.求:
(2011?北京二模)如图所示电路,设电源电压不变,灯丝电阻不随温度变化,滑动变阻器的最大阻值为R.当开关S1、S2断开,滑动变阻器的滑片P位于A端时,电压表V2示数为U2,电阻R2和滑动变阻器消耗的总功率为P1=2.4W;当开关S1断开,S2闭合时,电压表V1示数为U1,灯正常发光,电流表的示数为I;当开关S1、S2都闭合时,接入电路的滑动变阻器阻值为最大值的2/3时,电流表的示数与I相比变化了△I=1.4A,滑动变阻器消耗的电功率为P2=14.7W.已知U1:U2=7:6.求:查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示电路,设电源电压不变.当只闭合开关S1时,电流表的示数是I1;当只闭合开关S2时,电流表的示数是I2;已知I1:I2=2:1.当通过控制开关S1和S2,使电路消耗的最大功率和最小功率分别为P总和P总′,已知电路消耗的总功率达到最小时,电压表V1、V2的示数之比为2:1,电阻R2消耗的电功率P2′为2W,求:
如图所示电路,设电源电压不变.当只闭合开关S1时,电流表的示数是I1;当只闭合开关S2时,电流表的示数是I2;已知I1:I2=2:1.当通过控制开关S1和S2,使电路消耗的最大功率和最小功率分别为P总和P总′,已知电路消耗的总功率达到最小时,电压表V1、V2的示数之比为2:1,电阻R2消耗的电功率P2′为2W,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com