
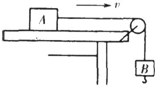
 如图所示,木块A的质量为m1,一端与水平细绳相连,细绳的另一端挂着质量为m2(m2<m1)的钩码B,木块恰好在桌面上匀速运动.若在A上再加一个质量为m的砝码,同时在日下再挂上一个质量为m的钩码,木块的速度将
如图所示,木块A的质量为m1,一端与水平细绳相连,细绳的另一端挂着质量为m2(m2<m1)的钩码B,木块恰好在桌面上匀速运动.若在A上再加一个质量为m的砝码,同时在日下再挂上一个质量为m的钩码,木块的速度将 ①.
①.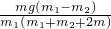


科目:初中物理 来源: 题型:

查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,光滑水平面上有质量分别为m1和m2的甲、乙两木块,两木块中间用一原长为L、劲度系数为k的轻质弹簧连接起来,现用一水平力F向左推木块乙,当两木块一起匀加速运动时,两木块之间的距离是( )
如图所示,光滑水平面上有质量分别为m1和m2的甲、乙两木块,两木块中间用一原长为L、劲度系数为k的轻质弹簧连接起来,现用一水平力F向左推木块乙,当两木块一起匀加速运动时,两木块之间的距离是( )查看答案和解析>>
科目:初中物理 来源: 题型:单选题
查看答案和解析>>
科目:初中物理 来源:《11.1 固体压强》2013年同步练习(丹阳市云阳学校)(解析版) 题型:选择题
查看答案和解析>>
科目:初中物理 来源:《第9章 压力和压强》2011年单元测试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com