
 ×100%=
×100%=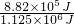 ×100%=78.4%.
×100%=78.4%.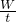 =
=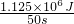 =2.25×104W.
=2.25×104W. ×100%得到机械效率;
×100%得到机械效率; 得到拉力的功率.
得到拉力的功率.

科目:初中物理 来源: 题型:多选题
查看答案和解析>>
科目:初中物理 来源: 题型:单选题
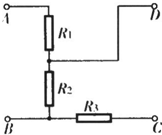 如图所示,三个定值电阻R1、R2、R3的电阻值均不相等,在A、B之间接一个电源,在C、D之间接一个电流表,电流表的示数为I,现将电源、电流表的位置互调,则电流表的示数
如图所示,三个定值电阻R1、R2、R3的电阻值均不相等,在A、B之间接一个电源,在C、D之间接一个电流表,电流表的示数为I,现将电源、电流表的位置互调,则电流表的示数查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 电阻R1、R2并联后接到电源上,R1 =40Ω,R2 =60Ω.开关闭合后,电阻R1消耗的电功率为3.6W.
电阻R1、R2并联后接到电源上,R1 =40Ω,R2 =60Ω.开关闭合后,电阻R1消耗的电功率为3.6W.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com