
 小明用如图所示的滑轮组提升重物.第一次提升一件,所用的拉力F1=3N;第二次增加一件相同重物;所用的拉力F2=5N,两次均将重物匀速提升0.2m.不计摩擦与绳子的重力,求:
小明用如图所示的滑轮组提升重物.第一次提升一件,所用的拉力F1=3N;第二次增加一件相同重物;所用的拉力F2=5N,两次均将重物匀速提升0.2m.不计摩擦与绳子的重力,求: (G+G动)…①
(G+G动)…① (2G+G动)…②
(2G+G动)…② ×100%=
×100%= ×100%=
×100%= ×100%=
×100%= ×100%=80%.
×100%=80%.

 阅读快车系列答案
阅读快车系列答案科目:初中物理 来源: 题型:
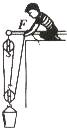 小明用如图所示的滑轮装置将总重为90N的重物匀速提升3m,此时他测得这个滑轮组的机械效率为75%.不计绳重和滑轮的摩擦阻力.
小明用如图所示的滑轮装置将总重为90N的重物匀速提升3m,此时他测得这个滑轮组的机械效率为75%.不计绳重和滑轮的摩擦阻力.查看答案和解析>>
科目:初中物理 来源: 题型:
 (2009?鼓楼区一模)小明用如图所示的滑轮组,在4s内将质量为60kg的物体A匀速提升了0.5m.已知绳子自由端所用的拉力F为200N.这个过程中拉力的功率为多大?每个滑轮多重?(g取10N/kg,大小滑轮重一样)
(2009?鼓楼区一模)小明用如图所示的滑轮组,在4s内将质量为60kg的物体A匀速提升了0.5m.已知绳子自由端所用的拉力F为200N.这个过程中拉力的功率为多大?每个滑轮多重?(g取10N/kg,大小滑轮重一样)查看答案和解析>>
科目:初中物理 来源: 题型:
 小明用如图所示的滑轮组将一个重为120N的物体匀速提升2m,所用的拉力为50N,此时拉力所做的功为W,滑轮组的机械效率为η1;若仍用该滑轮纽提升一个重为170N的物体.此时滑轮组的机械效率为η2,则W、η1.η2分别是多少?(不计绳重和摩擦)
小明用如图所示的滑轮组将一个重为120N的物体匀速提升2m,所用的拉力为50N,此时拉力所做的功为W,滑轮组的机械效率为η1;若仍用该滑轮纽提升一个重为170N的物体.此时滑轮组的机械效率为η2,则W、η1.η2分别是多少?(不计绳重和摩擦)查看答案和解析>>
科目:初中物理 来源:期中题 题型:计算题

查看答案和解析>>
科目:初中物理 来源:2006-2007学年北京市海淀区九年级(上)期中物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com