
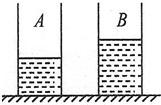
 如图所示,A、B是两个完全相同的薄壁柱形金属容器,质量为0.5kg,底面积为0.01m2,分别装有2×10-3m3的水和3.0×10-3 m3的酒精(ρ酒精=0.8×103 kg/m3).将一小球分别放入A、B中(足可以浸没小球),静止后所受到的浮力分别为1N和0.9N.(g取10N/kg)
如图所示,A、B是两个完全相同的薄壁柱形金属容器,质量为0.5kg,底面积为0.01m2,分别装有2×10-3m3的水和3.0×10-3 m3的酒精(ρ酒精=0.8×103 kg/m3).将一小球分别放入A、B中(足可以浸没小球),静止后所受到的浮力分别为1N和0.9N.(g取10N/kg)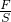 =
=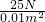 =2500Pa,
=2500Pa, =
=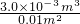 =0.3m,
=0.3m,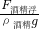 =
=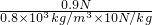 =1.125×10-4m3,
=1.125×10-4m3, =
= =0.1Kg,
=0.1Kg, =
= ≈0.89×103kg/m3,
≈0.89×103kg/m3,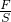 可求对地面的压强.
可求对地面的压强.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中物理 来源: 题型:
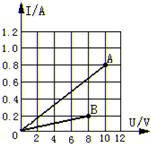 如图所示,A、B是两个电阻的电压-电流关系图象,根据该图象求:
如图所示,A、B是两个电阻的电压-电流关系图象,根据该图象求:查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,A、B是两个密闭的球形容器,C、D、E都是两端开口的玻璃管,它们与容器接口处紧密封接.容器A、B和玻璃管D、E内盛有水,各水面高度差如图所示.则E管内水面高出B容器水面的高度h应等于( )
如图所示,A、B是两个密闭的球形容器,C、D、E都是两端开口的玻璃管,它们与容器接口处紧密封接.容器A、B和玻璃管D、E内盛有水,各水面高度差如图所示.则E管内水面高出B容器水面的高度h应等于( )查看答案和解析>>
科目:初中物理 来源: 题型:
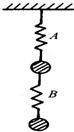 如图所示,A、B是两个完全相同的轻弹簧.当在弹簧上作用1N的拉力时,两弹簧都能伸长0.5cm,图中的两只球重都是3N,则两条弹簧的伸长之和是( )
如图所示,A、B是两个完全相同的轻弹簧.当在弹簧上作用1N的拉力时,两弹簧都能伸长0.5cm,图中的两只球重都是3N,则两条弹簧的伸长之和是( )| A、1.5cm | B、3cm | C、4.5cm | D、6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com