
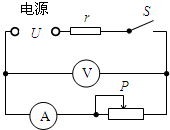
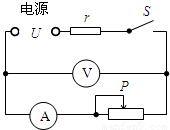
 图示电路中,电源的电压为U,r为定值电阻,闭合开关,调节滑动变阻器,当电压表示数U1=105V时,电流表示数I1=1A,当电压表示数U2=100V时,电流表示数I2=2A.
图示电路中,电源的电压为U,r为定值电阻,闭合开关,调节滑动变阻器,当电压表示数U1=105V时,电流表示数I1=1A,当电压表示数U2=100V时,电流表示数I2=2A.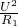 -P散)t1=Q吸-------③
-P散)t1=Q吸-------③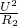 -P散)t2=Q吸--------④
-P散)t2=Q吸--------④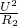 t1+Q吸-
t1+Q吸-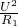 t1)t2=t1Q吸,
t1)t2=t1Q吸,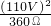 ×9×60s+31500J-
×9×60s+31500J-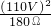 ×9×60s)t2=31500J×9×60s,
×9×60s)t2=31500J×9×60s, t表示出两种电阻的电功,根据Q=cm△t求出水吸收的热量列出等式,解之即可得出第二个电水壶加热的时间.
t表示出两种电阻的电功,根据Q=cm△t求出水吸收的热量列出等式,解之即可得出第二个电水壶加热的时间.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中物理 来源: 题型:
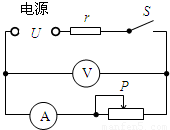
 图示电路中,电源的电压为U,r为定值电阻,闭合开关,调节滑动变阻器,当电压表示数U1=105V时,电流表示数I1=1A,当电压表示数U2=100V时,电流表示数I2=2A.
图示电路中,电源的电压为U,r为定值电阻,闭合开关,调节滑动变阻器,当电压表示数U1=105V时,电流表示数I1=1A,当电压表示数U2=100V时,电流表示数I2=2A.查看答案和解析>>
科目:初中物理 来源:2013年湖北省黄冈市自主招生预录物理模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
科目:初中物理 来源:2011年安徽省蚌埠二中高一自主招生考试物理试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中物理 来源:2011年安徽省蚌埠市普通高中高一自主招生考试物理试卷(解析版) 题型:解答题
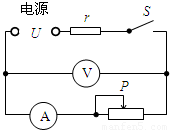
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com