
 ,m甲=m乙,
,m甲=m乙,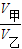 =
= =
= =
= ,故A不正确;
,故A不正确; =
= ≠
≠ ,故C不正确;
,故C不正确; =
= =
= ,即甲、乙两球所受的浮力之比为3:2,故D正确;
,即甲、乙两球所受的浮力之比为3:2,故D正确;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 两个完全相同的圆柱形容器中,分别盛有质量相等的煤油和水,如图所示,已知图中液体内M、N两点到容器底部的距离相等,煤油的密度小于水的密度.设M、N两点处的液体压强分别为pM和pN,则这两处的液体压强大小关系是( )
两个完全相同的圆柱形容器中,分别盛有质量相等的煤油和水,如图所示,已知图中液体内M、N两点到容器底部的距离相等,煤油的密度小于水的密度.设M、N两点处的液体压强分别为pM和pN,则这两处的液体压强大小关系是( )查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,两个完全相同的圆柱形容器内盛有不同的液体A和B(已知ρA<ρB),将实心金属球甲浸没在液体A中、实心金属球乙浸没在液体B中,且均无液体溢出,这时A、B两液体对容器底部的压强大小相等,则可以确定( )
如图所示,两个完全相同的圆柱形容器内盛有不同的液体A和B(已知ρA<ρB),将实心金属球甲浸没在液体A中、实心金属球乙浸没在液体B中,且均无液体溢出,这时A、B两液体对容器底部的压强大小相等,则可以确定( )查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,两个完全相同的圆柱形容器内装有深度不同的甲、乙两种液体放在水平桌面上,已知两个容器底所受液体的压强相等;现将两个完全相同的金属球分别投入两容器中都浸没,且两容器均没有液体溢出,这时甲、乙液体对容器底的压强关系是
如图所示,两个完全相同的圆柱形容器内装有深度不同的甲、乙两种液体放在水平桌面上,已知两个容器底所受液体的压强相等;现将两个完全相同的金属球分别投入两容器中都浸没,且两容器均没有液体溢出,这时甲、乙液体对容器底的压强关系是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com