
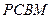 是直角梯形,∠
是直角梯形,∠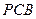 =90°,
=90°,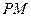 ∥
∥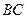 ,
,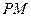 =1,
=1,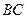 =2,又
=2,又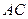 =1,∠
=1,∠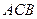 =120°,
=120°,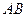 ⊥
⊥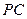 ,直线
,直线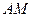 与直线
与直线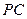 所成的角为60°.
所成的角为60°.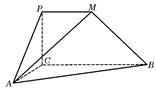
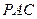 ⊥平面
⊥平面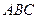 ;
;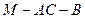 的余弦值.
的余弦值. 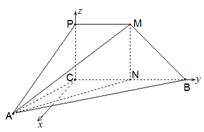
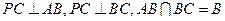 ,所以
,所以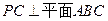 .
.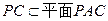 ,
,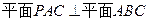 . …………………………………3分
. …………………………………3分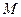 在面
在面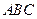 内的射影
内的射影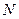 必在
必在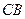 上,易知
上,易知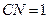 .
. 与直线
与直线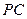 所成的角为
所成的角为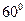 ,所以
,所以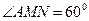 .
.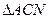 中,由余弦定理得
中,由余弦定理得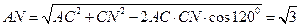 .
.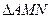 中,
中,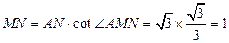 . …………………………….5分
. …………………………….5分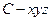 .
.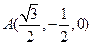 ,
,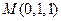 .
.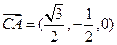 ,
,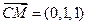 .
. 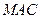 的一个法向量为
的一个法向量为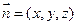 ,
,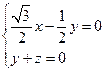 .
.
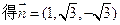 . …………………………………………………9分
. …………………………………………………9分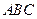 的一个法向量为
的一个法向量为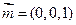 . ………………………………………….10分
. ………………………………………….10分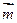 与
与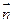 所成的角为
所成的角为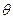 ,则
,则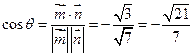 . ……………………..11分
. ……………………..11分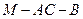 为锐角,故二面角
为锐角,故二面角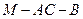 的余弦值为
的余弦值为 .
. 

 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中英语 来源: 题型:
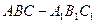 中, AC=4,CB=2,AA1=2
中, AC=4,CB=2,AA1=2
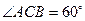 ,E、F分别是
,E、F分别是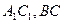 的中点。
的中点。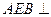 平面
平面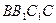 ;
;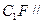 平面ABE;
平面ABE; 的体积。
的体积。查看答案和解析>>
科目:初中英语 来源: 题型:
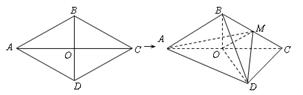
 的边长为
的边长为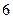 ,
, ,
,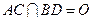 .将菱形
.将菱形 沿对角线
沿对角线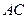 折起,得到三棱锥
折起,得到三棱锥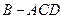 ,点
,点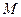 是棱
是棱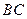 的中点,
的中点,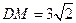 .
.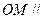 平面
平面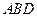 ;
;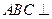 平面
平面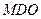 ;
;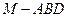 的体积.
的体积.查看答案和解析>>
科目:初中英语 来源: 题型:
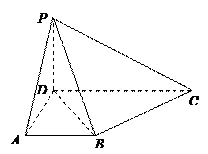
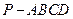 中,侧面
中,侧面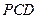
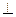 底面
底面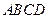 ,
,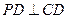 ,底面
,底面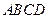 是直角梯形,
是直角梯形,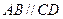 ,
,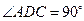 ,
,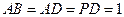 ,
,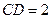 .
.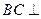 平面
平面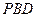 ;
; 为侧棱
为侧棱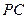 上一点,
上一点,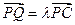 ,
,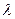 的值,使得二面角
的值,使得二面角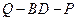 为
为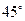 .
.查看答案和解析>>
科目:初中英语 来源: 题型:
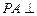 底面ABCD,底面为直角梯形,
底面ABCD,底面为直角梯形,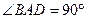 ,
,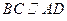 且AD=2,AB=BC=1,PA=
且AD=2,AB=BC=1,PA=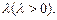
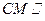 平面PAB;
平面PAB;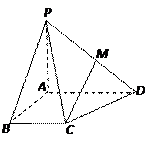
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com