
| ||||||
| 43 |
| 9 |
| 16 |
| 33 |
| 43 |
| 27 |
| 64 |
| ||
| 43 |
| 27 |
| 64 |
| ||
| 43 |
| 9 |
| 64 |
| 1 |
| 43 |
| 1 |
| 64 |
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |


科目:高中数学 来源:2010-2011年江西省宁冈中学高二第二学期期中考试理科数学 题型:解答题
本大题共13分)
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两 个岗位没有被选的概率;
个岗位没有被选的概率;
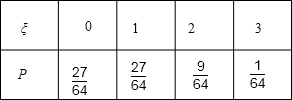
(2)设选择A岗位的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源:2010-2011年江西省高二第二学期期中考试理科数学 题型:解答题
本大题共13分)
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两个岗位没有被选的概率;
(2)设选择A岗位的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本大题共13分)
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两个岗位没有被选的概率;
(2)设选择A岗位的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源:2013届黑龙江虎林高中高二下学期期中理科数学试卷(解析版) 题型:解答题
三个求职者到某公司应聘,该公司为他们提供了A,B,C,D四个岗位,每人从中任选一个岗位。
(1)求恰有两个岗位没有被选的概率;
(2)设选择A岗位的人数为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
【解析】第一问利用古典概型概率公式得到记“恰有2个岗位没有被选”为事件A,则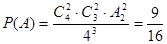
第二问中, 可能取值为0,1,2,3, 则
可能取值为0,1,2,3, 则 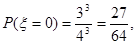
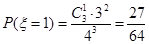 ,
,
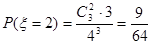 ,
, 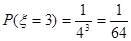
从而得到分布列和期望值。
解:(1)记“恰有2个岗位没有被选”为事件A,则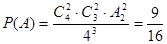 ……6分
……6分
(2) 可能取值为0,1,2,3,… 7分
可能取值为0,1,2,3,… 7分
则 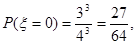
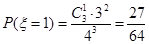 ,
,
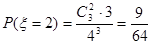 ,
, 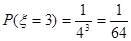
列出分布列 ( 1分)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com