
 ,正实数a、b、c满足f(c)<0<f(a)<f(b),若实数d是函数f(x)的一个零点,那么下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的个数为 .
,正实数a、b、c满足f(c)<0<f(a)<f(b),若实数d是函数f(x)的一个零点,那么下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的个数为 . 科目:高中数学 来源:2011年山东省实验中学高考数学一模试卷(文科)(解析版) 题型:选择题
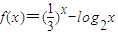 ,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为( )
,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为( )查看答案和解析>>
科目:高中数学 来源:2012年江苏省四星高中高三数学小题训练(16)(解析版) 题型:解答题
 ,正实数a、b、c成公差为正数的等差数列,且满足f(a)f(b)f(c)<0,若实数d是方程f(x)=0的一个解,那么下列四个判断:①d<a;②d>b;③d<c;④d>c中,有可能成立的个数为 .
,正实数a、b、c成公差为正数的等差数列,且满足f(a)f(b)f(c)<0,若实数d是方程f(x)=0的一个解,那么下列四个判断:①d<a;②d>b;③d<c;④d>c中,有可能成立的个数为 .查看答案和解析>>
科目:高中数学 来源:2011年四川省眉山市高考数学二模试卷(理科)(解析版) 题型:解答题
 ,正实数a、b、c成公差为正数的等差数列,满足f (a) f (b) f (c)<0,且实数d是方程f (x)=0的一个解.给出下列四个不等式:①d<a,②d>b,③d<c,④d>c,其中有可能成立的不等式的序号是 .
,正实数a、b、c成公差为正数的等差数列,满足f (a) f (b) f (c)<0,且实数d是方程f (x)=0的一个解.给出下列四个不等式:①d<a,②d>b,③d<c,④d>c,其中有可能成立的不等式的序号是 .查看答案和解析>>
科目:高中数学 来源:2009年广东省韶关市高考数学二模试卷(文科)(解析版) 题型:选择题
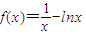 ,正实数a、b、c满足f(c)<0<f(a)<f(b),若实数d是函数f(x)的一个零点,那么下列四个判断:
,正实数a、b、c满足f(c)<0<f(a)<f(b),若实数d是函数f(x)的一个零点,那么下列四个判断:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com