
已知数列 的前n项的和为
的前n项的和为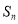 ,且
,且 ,
,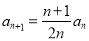
(1)证明数列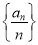 是等比数列
是等比数列
(2)求通项 公式及前n项的和
公式及前n项的和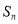 ;
;
(3)设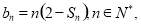 若集合M=
若集合M=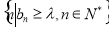 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围.
(1)见解析;(2)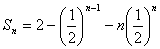 ;(3)
;(3)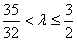
【解析】
试题分析:(1)等比数列的判定方法:定义法:若 是常数,则
是常数,则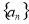 是等比数列;中项公式法:若数列
是等比数列;中项公式法:若数列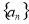 中,
中, ,则
,则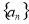 是等比数列;通项公式法:若数列通项公式可写成
是等比数列;通项公式法:若数列通项公式可写成 ;(2)一般地,如果数列
;(2)一般地,如果数列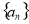 是等差数列,
是等差数列,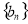 是等比数列,求数列
是等比数列,求数列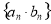 的前
的前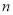 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列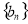 的公比,然后做差求解.(3)利用条件列式子,等比数列的性质及前
的公比,然后做差求解.(3)利用条件列式子,等比数列的性质及前 项和公式对函数与方程、等价转化、分类讨论等思想的运用,是高考的一种重要的考向.
项和公式对函数与方程、等价转化、分类讨论等思想的运用,是高考的一种重要的考向.
试题解析:(1)因为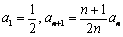 ,当
,当 时,
时,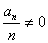 .又
.又 ,
,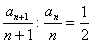 (
( )为常数,所以
)为常数,所以 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
(2)由 是以
是以 为首项,
为首项, 为公比的等比数列得,
为公比的等比数列得, 所以
所以 .
.
由错项相减得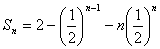 .
.
(3)因为 ,所以
,所以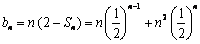 由于
由于
所以,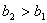 ,
, . 因为集合
. 因为集合 恰有4个元素,
恰有4个元素,
且 ,
, 所以
所以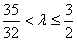 .
.
考点:等比数列判断,错位相减法及转化思想


科目:高中数学 来源:2014-2015学年福建省高二上学期第一阶段考试理科数学试卷(解析版) 题型:选择题
某校五四演讲比赛中,七位评委为一选手打出的分数如下:
90 86 90 97 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.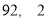 B.
B.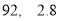 C.
C.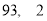 D.
D.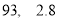
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期第一次检查文科数学试卷(解析版) 题型:选择题
已知等比数列 中,各项都是正数,且
中,各项都是正数,且 ,成等差数列,则
,成等差数列,则 =( )
=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二9月月考数学试卷试卷(解析版) 题型:填空题
在等比数列 中,
中, ,则数列
,则数列 的通项公式
的通项公式 _____________,设
_____________,设 ,则数列
,则数列 的前
的前 项和
项和 _____________.
_____________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二9月月考数学试卷试卷(解析版) 题型:选择题
在锐角 中,角
中,角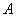 、
、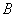 、
、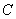 所对的边分别为
所对的边分别为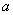 、
、 、
、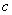 ,若
,若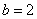 ,
, 且
且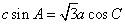 ,则
,则 的面积为( )
的面积为( )
A. B.
B.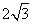 C.
C. D.
D.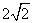
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com