
已知函数
 在
在 处取得极值
处取得极值 ,其中
,其中 为常数.
为常数.
(1)求 的值;
的值;
(2)讨论函数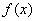 的单调区间;
的单调区间;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)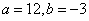
(2)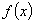 单调递减区间为
单调递减区间为 ,单调递增区间为
,单调递增区间为
(3)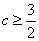 或
或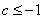
【解析】
试题分析:(1)利用函数的极值与导数的关系;(2)解决类似的问题时,函数在极值点处的导数为零,注意区分函数的最值和极值.求函数的最值时,要先求函数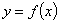 在区间
在区间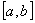 内使
内使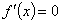 的点,再计算函数
的点,再计算函数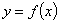 在区间内所有使
在区间内所有使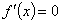 的点和区间端点处的函数值,最后比较即得.(3)恒成立的问题关键是分离参数,把所求问题转化为求函数的最值问题.(4)若可导函数
的点和区间端点处的函数值,最后比较即得.(3)恒成立的问题关键是分离参数,把所求问题转化为求函数的最值问题.(4)若可导函数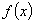 在指定的区间
在指定的区间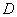 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为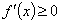
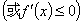 恒成立,从而构建不等式,要注意“=”是否可以取到.
恒成立,从而构建不等式,要注意“=”是否可以取到.
试题解析:解:(1)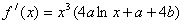 ,
,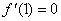 ,
,
∴
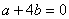 ,又
,又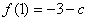 ,
,
∴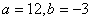 ; 5分
; 5分
(2)
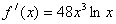 (
(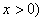
∴由 得
得 ,
,
当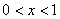 时,
时,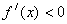 ,
,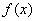 单调递减;
单调递减;
当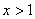 时,
时,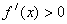 ,
,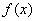 单调递增;
单调递增;
∴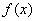 单调递减区间为
单调递减区间为 ,单调递增区间为
,单调递增区间为 9分
9分
由(2)可知, 时,
时,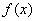 取极小值也是最小值
取极小值也是最小值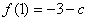 ,
,
依题意,只需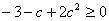 ,解得
,解得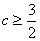 或
或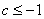 10分
10分
考点:(1)函数的导数与极值;(2)函数的导数与单调性;(3)函数恒成立的问题.


科目:高中数学 来源: 题型:
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8∶00~10∶00间各自的点击量,得如图所示的茎叶图,根据茎叶图回答下列问题.
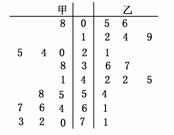
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两网站哪个更受欢迎?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
抛物线C的顶点在原点,焦点F与双曲线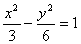 的右焦点重合,过点P(2,0)且斜率为1的直线
的右焦点重合,过点P(2,0)且斜率为1的直线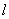 与抛物线C交于A,B两点,则弦AB的中点到抛物线准线的距离为_______
与抛物线C交于A,B两点,则弦AB的中点到抛物线准线的距离为_______
查看答案和解析>>
科目:高中数学 来源: 题型:
在航天员进行的一项太空实验中,要先后实施6个程序,其中程序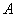 只能出现在第一步或最后一步,程序
只能出现在第一步或最后一步,程序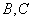 实施时必须相邻,请问实验顺序的编排方法共有 ( )
实施时必须相邻,请问实验顺序的编排方法共有 ( )
A.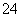 种 B.
种 B. 种 C.
种 C.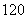 种 D.
种 D.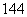 种
种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com