
(2009四川卷文)(本小题满分12分)
|
(I)求证:![]() ;
;
(II)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,
,
求证: ![]() ∥
∥![]()
(III)求二面角![]() 的大小。
的大小。
【解析】解法一:
因为平面ABEF⊥平面ABCD,BC![]() 平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF.
所以BC⊥EF.
因为⊿ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
 又因为∠AEF=45,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE.
因为BC![]() 平面ABCD, BE
平面ABCD, BE![]() 平面BCE,
平面BCE,
BC∩BE=B
所以![]()
…………………………………………6分
(II)取BE的中点N,连结CN,MN,则MN![]()
![]()
![]() PC
PC
∴ PMNC为平行四边形,所以PM∥CN.
∵ CN在平面BCE内,PM不在平面BCE内,
∴ PM∥平面BCE. …………………………………………8分
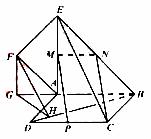
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.
作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,
作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.
∴ ∠FHG为二面角F-BD-A的平面角.
∵ FA=FE,∠AEF=45°,
∠AEF=90°, ∠FAG=45°.
设AB=1,则AE=1,AF=![]() ,则
,则![]()
在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+![]() =
=![]() ,
,
![]() ,
,
在Rt⊿FGH中, ![]() ,
,
∴ 二面角![]() 的大小为
的大小为![]()
…………………………………………12分
解法二: 因![]() 等腰直角三角形,
等腰直角三角形,![]() ,所以
,所以![]()
又因为平面![]() ,所以
,所以![]() ⊥平面
⊥平面![]() ,所以
,所以![]()
即![]() 两两垂直;如图建立空间直角坐标系,
两两垂直;如图建立空间直角坐标系,
(I) 设![]() ,则
,则![]() ,
,![]()
|
∵![]() ,∴
,∴![]() ,
,
从而![]()
![]() ,
,![]()
于是![]() ,
,![]()
∴![]()
![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]()
∵![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
∴![]()
(II)![]() ,从而
,从而![]()
于是![]()
∴![]() ⊥
⊥![]() ,又
,又![]() ⊥平面
⊥平面![]() ,直线
,直线![]() 不在平面
不在平面![]() 内,
内,
故![]() ∥平面
∥平面![]()
(III)设平面![]() 的一个法向量为
的一个法向量为![]() ,并设
,并设![]() =(
=(![]()
![]()
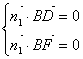 即
即
取![]() ,则
,则![]() ,
,![]() ,从而
,从而![]() =(1,1,3)
=(1,1,3)
取平面![]() D的一个法向量为
D的一个法向量为![]()
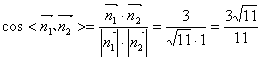
故二面角![]() 的大小为
的大小为![]()


科目:高中数学 来源: 题型:
(2009四川卷文)设矩形的长为![]() ,宽为
,宽为![]() ,其比满足
,其比满足![]() ∶
∶![]() =
=![]() ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009四川卷文)设矩形的长为![]() ,宽为
,宽为![]() ,其比满足
,其比满足![]() ∶
∶![]() =
=![]() ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009四川卷文)(本小题满分12分)
如图,正方形![]() 所在平面与平面四边形
所在平面与平面四边形![]() 所在平面互相垂直,△
所在平面互相垂直,△![]() 是等腰直角三角形,
是等腰直角三角形,![]()
(I)求证:![]() ;
;
(II)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,求证:
,求证: ![]() ∥
∥![]()
 (III)求二面角
(III)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009四川卷文)(本小题满分12分)
|
(I)求证:![]() ;
;
(II)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,
,
求证: ![]() ∥
∥![]()
(III)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高二上学期数学单元测试2-必修5第3章 题型:选择题
(2009四川卷文)已知 ,
, ,
, ,
, 为实数,且
为实数,且 >
> .则“
.则“ >
> ”是“
”是“ -
- >
> -
- ”的
( )
”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com