
在正方体ABCD-A1B1C1D1中,M、E、F、N分别是A1B1、B1C1、C1D1、D1A1的中点.
求证:(1)E、F、B、D四点共面;
(2)平面AMN∥平面EFDB.
|
解:(1)证明:如图,(1)连结B1D1.
∵E、F是B1C1、C1D1的中点,∴EF ∵D1D ∴D1B1∥DB.∴EF∥DB. ∴EF与DB确定一个平面. 故E、F、B、D四点共面. (2)∵M、N是A1B1、A1D1的中点, ∴MN∥D1B1∥EF. ∴MN∥平面EFDB. 连结NE,则NE ∴NEBA是平行四边形. ∴AN∥BE.∴AN∥平面BEDF. ∵AN、MN都在平面AMN内,且AN∩MN=N, ∴平面AMN∥平面EFBD. 方法归纳:证“面面平行”,要先证“线线平行”,进而要证“线面平行”,最后证得面面平行,这就是立体几何中最常用的化归思想(线线、线面及面面关系的相互转化). |
|
要证四点共面,可考虑确定平面的方法,而证明面面平行当然首先考虑判定定理. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.

 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.
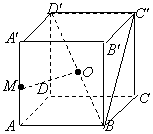
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(四川卷)解析版(文) 题型:解答题
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.

 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com