
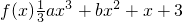 ,其中a≠0.
,其中a≠0.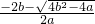 =
=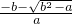 ,x2=
,x2= =
=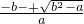 ,,
,,

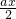 -
- ,x∈(0,1]恒成立,
,x∈(0,1]恒成立,
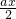 -
- ,g′(x)=-
,g′(x)=- +
+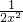 =
=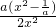 ,
, 或x=-
或x=- (舍去),
(舍去), <1,当x∈(0,
<1,当x∈(0, ]时g′(x)>0,g(x)=-
]时g′(x)>0,g(x)=-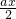 -
- 单调增函数;
单调增函数; ,1]时g′(x)<0,g(x)=-
,1]时g′(x)<0,g(x)=-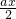 -
- 单调减函数,
单调减函数, 时,g(x)取得最大,最大值为g(
时,g(x)取得最大,最大值为g( )=-
)=- .
.
 ≥1,
≥1,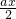 -
- 在区间(0,1]上单调递增,当x=1时g(x)最大,最大值为g(1)=-
在区间(0,1]上单调递增,当x=1时g(x)最大,最大值为g(1)=- ,
,
 ;
; ;
;

科目:高中数学 来源:2010年浙江省温州市苍南县龙港高中高考数学仿真模拟试卷(文科)(解析版) 题型:解答题
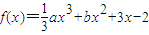 ,其中a≠0
,其中a≠0查看答案和解析>>
科目:高中数学 来源:2010年浙江省寿昌中学、新安江中学、严州中学高三第二次联考数学试卷(文科)(解析版) 题型:解答题
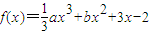 ,其中a≠0
,其中a≠0查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省5月第一次周考理科数学试卷(解析版) 题型:解答题
已知函数 =
= ,其中a≠0.
,其中a≠0.
(1)若对一切x∈R, ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函数 的图像上取定两点
的图像上取定两点 ,
,
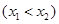 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使 成立?若存在,求
成立?若存在,求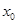 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(湖南卷解析版) 题型:解答题
已知函数 =
=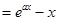 ,其中a≠0
,其中a≠0
(1)
若对一切x∈R, ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函数 的图像上取定两点
的图像上取定两点 ,
,
 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使 成立?若存在,求
成立?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题

 ,其中a≠0。
,其中a≠0。 ≥1恒成立,求a的取值集合。
≥1恒成立,求a的取值集合。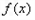 的图像上取定两点
的图像上取定两点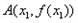 ,
,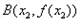
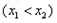 ,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使
,记直线AB的斜率为K,问:是否存在x0∈(x1,x2),使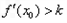 成立?若存在,求
成立?若存在,求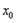 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com