Question

14．已知以点A（-1，2）为圆心的圆与直线l₁：x+2y+7=0相切，切点为P，过点B（-2，0）的动直线l与圆A相交于M，N两点，点M在x轴上方
（1）当|MN|=2$\sqrt{19}$时，求直线l的方程
（2）若△PBM的内切圆的圆心在x轴上，求以MN为直径的圆的方程．

Answer 1

分析 （1）根据相交弦长公式，求出圆心到直线的距离，设出直线方程，再根据点到直线的距离公式确定直线方程，
（2）设切点P（x₀，y₀），根据斜率公式以及切线的性质，求出切点坐标，再根据△PBM的内切圆的圆心在x轴上，求出直线l的方程，过点A作AD⊥MN，分别根据点到直线的距离公式求出圆A的半径和AD的长度，继而求出以MN为直径的圆的半径，求出直线AD的方程和，直线l的交点坐标即是以MN为直径的圆的圆心坐标，根据圆的标准方程即可求出答案．

解答 解：（1）设直线l的方程是x=my-2或y=0，
∵d_{圆心到直线}=$\sqrt{{R}^{2}-（\frac{|MN|}{2}）^{2}}$=1
∴$\frac{|-1-2m+2|}{\sqrt{1+{m}^{2}}}$=1⇒3m²-4m=0⇒m=0或，y=0不成立，
∴直线l的方程是：x=-2或3x-4y+6=0，
（2）设切点P（x₀，y₀），则k_AP=$\frac{{y}_{0-2}}{{x}_{0}+1}$，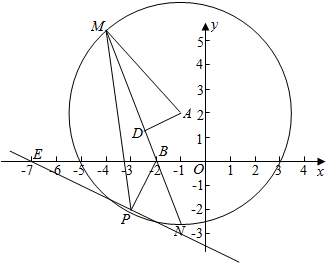
又k_l1=-$\frac{1}{2}$，
∴$\frac{{y}_{0-2}}{{x}_{0}+1}$•（-$\frac{1}{2}$）=-1，即y₀=2x₀+4，①
又x₀+2y₀+7=0，②，
由①②解得$\left\{\begin{array}{l}{{x}_{0}=-3}\\{{y}_{0}=-2}\end{array}\right.$，∴P（-3，-2），又∵B（-2，0）
∴k_BP=$\frac{-2-0}{-3-（-2）}$=2，
∵△PBM的内切圆的圆心在x轴上，
∴∠MBE=∠PBE
∴k_BM=-k_PB=-2，
∴直线L的方程为y-0=-2（x+2），即2x+y+4=0，③
∵A（-1，2），
∴R=$\frac{|-1+4+7|}{\sqrt{{1}^{2}+{2}^{2}}}$=2$\sqrt{5}$，
过点A作AD⊥MN，
∴AD=$\frac{|-2+2+4|}{\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$，
∴DM²=AM²-AD²=$\frac{84}{5}$，
∵k_AD•k_BM=-1，
∴k_AD=$\frac{1}{2}$，
∴直线AD的方程为y-2=$\frac{1}{2}$（x+1），即x-2y+5=0，④，
由③④构成方程组，解得$\left\{\begin{array}{l}{x=-\frac{13}{5}}\\{y=\frac{6}{5}}\end{array}\right.$，
∴以MN为直径的圆的圆心坐标为（-$\frac{13}{5}$，$\frac{6}{5}$），
∴以MN为直径的圆的方程为（x+$\frac{13}{5}$）²+（y-$\frac{6}{5}$）²=$\frac{84}{5}$．

点评 本题考查了直线和圆的位置关系，点到直线的距离公式，以及圆的方程的求法，直线方程的求法，关键是求出关键点的坐标，本题的运算能力要求很高，需要认真仔细，属于中档题．