
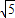 ,则tanα= .
,则tanα= .  cosα,再利用同角三角函数间的基本关系切化弦后,将得出的关系式代入计算,即可求出值.
cosα,再利用同角三角函数间的基本关系切化弦后,将得出的关系式代入计算,即可求出值.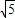 两边平方得:(2cosα-sinα)2=5,
两边平方得:(2cosα-sinα)2=5, cosα,
cosα,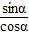 =-
=- .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com