
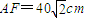 .
.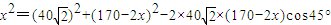 .
.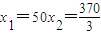 .
.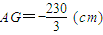 (不合题意,舍去).
(不合题意,舍去).

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
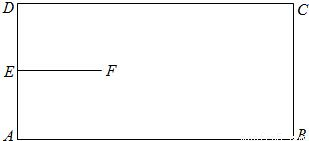
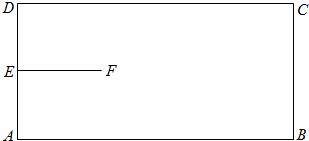
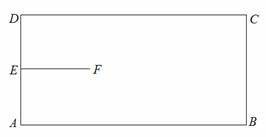
如图,矩形ABCD是机器人踢球的场地,AB=170cm,AD=80cm,机器人先从AD中点E进入场地到点F处,EF=40cm,EF⊥AD。场地内有一小球从B点向A点运动,机器人从F点出发去截小球。现机器人和小球同时出发,它们均作直线运动,并且小球运动的速度是机器人行走速度的2倍。若忽略机器人圆底旋转所需的时间,则机器人最快可在何处截住小球?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省盐城市大冈中学高三学情分析数学试卷(1)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:江苏省南京市2010届高三上学期期末考试 题型:解答题
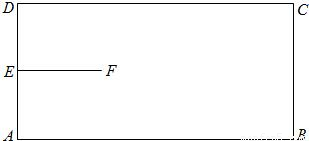
如图,矩形ABCD是机器人踢球的场地,AB=170cm,AD=80cm,机器人先从AD中点E进入场地到点F处,EF=40cm,EF⊥AD。场地内有一小球从B点向A点运动,机器人从F点出发去截小球。现机器人和小球同时出发,它们均作直线运动,并且小球运动的速度是机器人行走速度的2倍。若忽略机器人圆底旋转所需的时间,则机器人最快可在何处截住小球?
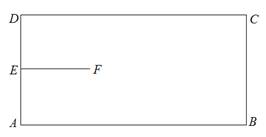
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com