Question

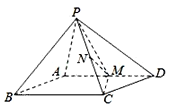
【题目】如图，已知四棱锥P-ABCD的底面ABCD是平行四边形，PA⊥平面ABCD．M是AD的中点，N是PC的中点．

（1）求证：MN∥平面PAB；

（2）若平面PMC⊥平面PAD，求证：CM⊥AD；

（3）若平面ABCD是矩形，PA=AB，求证：平面PMC⊥平面PBC．

Answer 1

【答案】（1）见解析（2）见解析（3）见解析

【解析】

（1）取PB的中点E，连接EN，AE，证明MN∥AE，即证MN∥平面PAB；（2）假设CM与AD不垂直，在平面ABCD内过M作AD的垂线，交BC于Q，连接PQ，MQ，证明平面PMQ⊥平面PAD，显然这与平面PMC⊥平面PAD矛盾．故原题得证；（3）先证明MN⊥平面PBC，即证平面PMC⊥平面PBC．

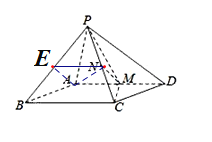
证明：（1）取PB的中点E，连接EN，AE．

∵E，N分别是PB，PC的中点，∴ENBC，ENBC，

∵M是AD的中点，四边形ABCD是平行四边形，

∴AMBC ,AMBC，

∴ENAM，ENAM，∴四边形AMNE是平行四边形，

∴MN∥AE，

又MN平面PAB，AE平面PAB，

∴MN∥平面PAB．

（2）假设CM与AD不垂直，在平面ABCD内过M作AD的垂线，交BC于Q，连接PQ，MQ，

∵PA⊥平面ABCD，MQ平面ABCD，

∴PA⊥MQ，又AD⊥MQ，PA∩AD=A，

∴MQ⊥平面PAD，又MQ平面PMQ，

∴平面PMQ⊥平面PAD，

显然这与平面PMC⊥平面PAD矛盾．

故假设不成立，∴CM⊥AD．

（3）∵四边形ABCD是矩形，∴AD⊥AB，

∵PA⊥平面ABCD，AD平面ABCD，

∴PA⊥AD，又PA∩AB=A，

∴AD⊥平面PAB，∴AD⊥AE，

由（1）可知四边形AMNE是平行四边形，

∴四边形AMNE是矩形，

∴MN⊥EN，

又AM=MD，PA=AB=CD，∠PAM=∠MDC=90°，

∴△PMA≌△CMD，

∴PM=CM，又N是PC的中点，

∴MN⊥PC，

又PC∩EN=N，PC平面PBC，EN平面PBC，

∴MN⊥平面PBC，又MN平面PMC，

∴平面PMC⊥平面PBC．