
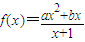 ,曲线y=f(x)在点(1,f(1))处的切线方程是5x-4y+1=0.
,曲线y=f(x)在点(1,f(1))处的切线方程是5x-4y+1=0.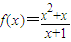 ,
,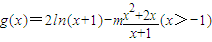 ,求导函数,构建新函数h(x)=-mx2+(2-2m)x+2-2m,分类讨论,确定g(x)在[0,+∞)上的单调性,即可得到结论.
,求导函数,构建新函数h(x)=-mx2+(2-2m)x+2-2m,分类讨论,确定g(x)在[0,+∞)上的单调性,即可得到结论.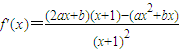 .
.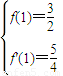 ,∴
,∴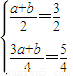 ,∴
,∴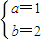 -------(4分)
-------(4分)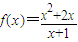 ,∴
,∴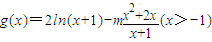 ,则
,则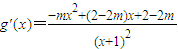 ,--------------------------(6分)
,--------------------------(6分)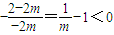 且h(0)=2-2m>0
且h(0)=2-2m>0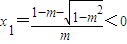 ;
;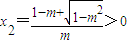


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:高考真题 题型:解答题
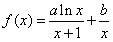 ,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0,
,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0, 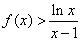 .
. 查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题
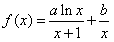 ,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0,
,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0,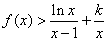 ,求k的取值范围。
,求k的取值范围。 查看答案和解析>>
科目:高中数学 来源:2011年《金版新学案》高三数学(文科)一轮复习测评卷:章末质量检测11(解析版) 题型:解答题
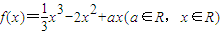 在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直.
在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直.查看答案和解析>>
科目:高中数学 来源:2008年北京市丰台区高考数学一模试卷(文科)(解析版) 题型:解答题
 在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直.
在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com