
已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
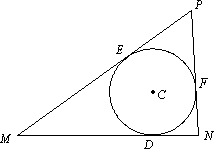
(Ⅰ)建立适当的直角坐标系,求点P的轨迹方程;
(Ⅱ)过点M作直线l与所求轨迹交于两个不同的点A、B,若(![]() +λ
+λ![]() )·(
)·(![]() -λ
-λ![]() )=0,且λ∈[2-
)=0,且λ∈[2-![]() ,2+
,2+![]() ],求直线l与直线MN夹角
],求直线l与直线MN夹角![]() 的取值范围.
的取值范围.
|
解:(Ⅰ)以直线MN为x轴,MN的中点为坐标原点O, 建立直角坐标系xOy. 1分 ∵PM-PN=(PE+EM)-(PF+FN)=MD-ND=2 或PM-PN=(PE+EM)-(PF+FN)=MD-ND=-2 3分 ∴点P的轨迹是以M、N为焦点,实轴长为2的双曲线(不包含顶点), 其轨迹方程为 (Ⅱ)∵( ∴ 设A(x1,y1),B(x2,y2),则 设AB:my=x+2,代入 即(3m2-1)y2-12my+9=0. ∴ ①当 ∴ ∴ ②当 ∵λ∈[2- ∴ ∴ 由①、②得tan2 则夹角 ∵tan ∴ |


科目:高中数学 来源: 题型:
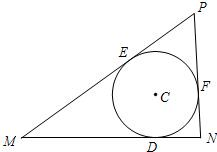 已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.| MA |
| MB |
| MA |
| MB |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2007年苏、锡、常、镇四市高三教学情况调查(一)数学 题型:044
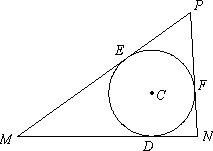
已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
(Ⅰ)建立适当的直角坐标系,求点P的轨迹方程;
(Ⅱ)过点M作直线l与所求轨迹交于两个不同的点A、B,若(![]() +λ
+λ![]() )·(
)·(![]() -λ
-λ![]() )=0,且λ∈[2-
)=0,且λ∈[2-![]() ,2+
,2+![]() ],求直线l与直线MN夹角θ的取值范围.
],求直线l与直线MN夹角θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
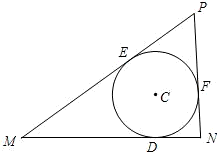 已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P. +λ
+λ )•(
)•( -λ
-λ )=0,且λ∈[2-
)=0,且λ∈[2- ,2+
,2+ ],求直线l与直线MN夹角θ的取值范围.
],求直线l与直线MN夹角θ的取值范围.查看答案和解析>>
科目:高中数学 来源:2010年甘肃省河西各校高考数学一模试卷(理科)(解析版) 题型:解答题
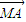 +λ
+λ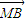 )•(
)•(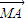 -λ
-λ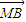 )=0,且λ∈[2-
)=0,且λ∈[2-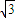 ,2+
,2+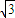 ],求直线l与直线MN夹角θ的取值范围.
],求直线l与直线MN夹角θ的取值范围.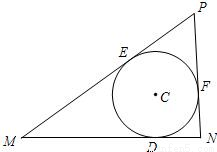
查看答案和解析>>
科目:高中数学 来源:2007年江苏省苏锡常镇四市高考数学一模试卷(解析版) 题型:解答题
 +λ
+λ )•(
)•( -λ
-λ )=0,且λ∈[2-
)=0,且λ∈[2- ,2+
,2+ ],求直线l与直线MN夹角θ的取值范围.
],求直线l与直线MN夹角θ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com