
分析:本题以数列为载体,主要考查观察、分析、归纳的能力和数学归纳法.应先通过数列的结构特征进行观察和分析,猜想出Sn的公式,再对Sn的公式用数学归纳法论证.前一部分是基础,后一部分是发展.这种“先猜想,后论证”的题型正是近几年高考的探索性题型,有利于培养创新意识和创造性思维,是热点之一.用数学归纳法证题的关键是如何利用归纳假设.在利用归纳假设进行化简过程中,要时刻瞄准n=k+1时等式右边这一目标.
解:∵分母依次是3,5,7,9的平方数,分子比分母小1,由此猜想![]() .证明如下:
.证明如下:
(1)当n=1时,![]() ,等式成立;
,等式成立;
(2)设当n=k时,等式成立,
即![]() .
.
则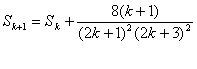
![]()
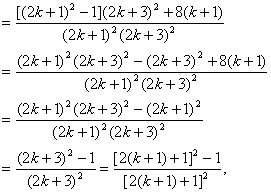
即当n=k+1时,等式也成立.
根据(1)、(2),可知等式对任何n∈N*都成立.
点评 数学归纳法通常用来证明与正整数有关的命题,它属于完全归纳法,有两个基本步骤:
第一步是起始步,证明当n取第一个值n0(n0是使结论成立的最小的正整数)时,结论正确;
第二步是假设步,假设n=k(k∈N*,且k≥n0)时结论正确,证明n=k+1时,结论也正确.
其中第一步是递推的基础,第二步是递推的依据,两者相辅相成,缺一不可.


科目:高中数学 来源:2010-2011学年黑龙江省哈尔滨市高三第三次模拟理科数学试题 题型:选择题
已知数列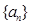 为等差数列,
为等差数列, 其前n项和,且
其前n项和,且 等于
等于
A.25 B.27 C.50 D.54
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com