练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

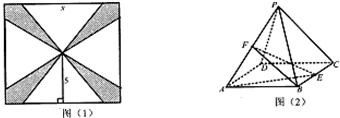
    点E、F分别是三棱锥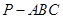的棱AP、BC的中点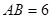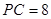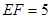，，，，则异面直线AB与PC所成的角为                              （     ）

    A． 60°       B．45°        C．30°       D．90°

     

    【答案】

    D

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    一块边长为10cm的正方形铁片按图（1）中所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个如图（2）所示的正四棱锥形容器．在图（1）中，x表示等腰三角形的底边长；在图（2）中，点E、F分别是四棱锥P-ABCD的棱BC，PA的中点，
    （1）证明：EF∥平面PDC；
    （2）把该容器的体积V表示为x的函数，并求x=8cm时，三棱锥A一BEF的体积．

    查看答案和解析>>

    科目：高中数学 来源：北京东城区2000～2001学年度第二学期形成性测试 高三数学 (六)立体几何 题型：013

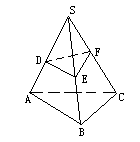
    如图，D、E、F分别是三棱锥S－ABC侧棱SA、SB、SC上的点，且SD∶DA=SE∶EB=CF∶FS=2∶1，那么过D、E、F的平面截三棱锥S－ABC所得上下两部分体积的比为

    [　　]

    A．4∶31

    B．6∶23

    C．4∶23

    D．2∶25

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一块边长为10cm的正方形铁片按图（1）中所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个如图（2）所示的正四棱锥形容器．在图（1）中，x表示等腰三角形的底边长；在图（2）中，点E、F分别是四棱锥P-ABCD的棱BC，PA的中点，
    （1）证明：EF∥平面PDC；
    （2）把该容器的体积V表示为x的函数，并求x=8cm时，三棱锥A一BEF的体积．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年河南省中原名校高三（上）第三次联考数学试卷（文科）（解析版） 题型：解答题

    一块边长为10cm的正方形铁片按图（1）中所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个如图（2）所示的正四棱锥形容器．在图（1）中，x表示等腰三角形的底边长；在图（2）中，点E、F分别是四棱锥P-ABCD的棱BC，PA的中点，
    （1）证明：EF∥平面PDC；
    （2）把该容器的体积V表示为x的函数，并求x=8cm时，三棱锥A一BEF的体积．

    查看答案和解析>>

    同步练习册答案