
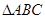 中,“
中,“ ”是“
”是“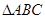 为直角三角形”的
为直角三角形”的| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分又不必要条件 |
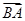 与
与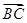 的夹角为α,利用平面向量的数量积运算法则化简
的夹角为α,利用平面向量的数量积运算法则化简 ?
? 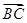 ,由已知
,由已知 ?
? 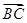 =0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立.
=0,得到cosα值为0,由α的范围,利用特殊角的三角函数值求出α为直角,可得三角形ABC为直角三角形;反过来,若三角形ABC为直角三角形,但不一定B为直角,故必要性不一定成立. ?
? 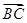 =0时,
=0时,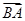 与
与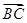 的夹角为α,
的夹角为α, ?
? 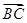 =ac?cos(π-α)=-ac?cosα,
=ac?cos(π-α)=-ac?cosα, ?
? 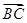 =0,
=0,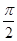 ,
, ?
? 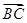 不一定等于0,
不一定等于0, ?
? 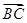 =0”是“△ABC为直角三角形”的充分不必要条件.
=0”是“△ABC为直角三角形”的充分不必要条件.

科目:高中数学 来源:不详 题型:单选题

| A.200 m | B.300 m |
| C.400 m | D.100 m |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 距A处8处有一走私船,正沿东偏南
距A处8处有一走私船,正沿东偏南 的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以
的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以 海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。
海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇航行方向。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 ,求实数m的值。
,求实数m的值。 ,求△ABC面积的最大值.
,求△ABC面积的最大值. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com