
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省琼海市高三第一学期期末理科数学试卷 题型:解答题
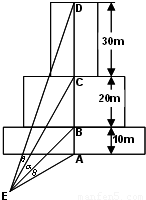
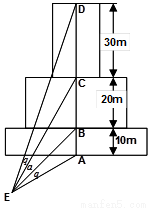
如图为一建筑物的正视图,尺寸图中标出,为了做好火灾的防备工作,需要在地面上确定安装喷水枪的地点 ,经测试只有当
,经测试只有当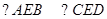 (图中的
(图中的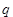 角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点
角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点 到建筑物的距离
到建筑物的距离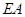 长.(注:图中
长.(注:图中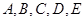 在同一个平面内;不考虑喷水枪的高度.)
在同一个平面内;不考虑喷水枪的高度.)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
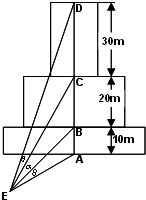
如图为一建筑物的正视图,尺寸图中标出,为了做好火灾的防备工作,需要在地面上确定安装喷水枪的地点![]() ,经测试只有当
,经测试只有当![]() (图中的
(图中的![]() 角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点
角)时,才能使得水枪喷射能够覆盖整个建筑物,求水枪安装点![]() 到建筑物的距离
到建筑物的距离![]() 长.(注:图中
长.(注:图中![]() 在同一个平面内;不考虑喷水枪的高度.)
在同一个平面内;不考虑喷水枪的高度.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com