Question

2．若变量x，y满足约束条件$\left\{\begin{array}{l}x+2y-2≥0\\ 2x+y-4≤0\\ 4x-y+1≥0\end{array}\right.$，则目标函数z=y-2x的最大值是（　　）

• A． $\frac{3}{2}$
• B． 2
• C． 3
• D． $\frac{5}{2}$

Answer 1

分析 画出满足条件的可行域，求出各个角点的坐标，代和目标函数比较大小后，可得目标函数z=y-2x的最大值．

解答 解：满足约束条件$\left\{\begin{array}{l}x+2y-2≥0\\ 2x+y-4≤0\\ 4x-y+1≥0\end{array}\right.$的可行域如下图所示：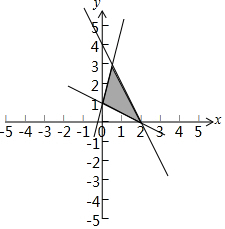

由$\left\{\begin{array}{l}2x+y-4=0\\ 4x-y+1=0\end{array}\right.$得：$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=3\end{array}\right.$，
当x=0，y=1时，目标函数z=y-2x=1；
当x=2，y=0时，目标函数z=y-2x=-4；
当x=$\frac{1}{2}$，y=3时，目标函数z=y-2x=2；
故目标函数z=y-2x的最大值是2，
故选：B

点评 本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解