练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)在x＝x0处的导数不存在，则曲线y＝f(x)

    [　　]
    A．

    在点[x0，f(x0)]处的切线不存在

    B．

    在点[x0，f(x0)]处的切线可能存在

    C．

    在点x0处不连续

    D．

    在x＝x0处连续

    答案：B
    解析：

    函数在某一点处的导数实际上就是相应函数图象在该点切线的斜率，深刻理解概念是正确解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黄冈重点作业·高三数学（下） 题型：013

    设函数f(x)在x＝x0处可导，则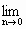的值

    [　　]

    A．与x0，n都有关

    B．仅与x0有关

    C．仅与n有关

    D．与x0，n都无关

    查看答案和解析>>

    科目：高中数学 来源：101网校同步练习　高二数学　苏教版(新课标·2004年初审) 苏教版 题型：013

    设函数f(x)在x＝x0处有导数，且1，则f’(x0)＝

    [　　]

    A．1

    B．0

    C．2

    D．

    查看答案和解析>>

    科目：高中数学 来源：天津市耀华中学2012届高三寒假验收考试数学文科试题 题型：013

    设函数f(x)＝x|x|＋bx＋c，则下列命题中正确命题的序号有

    ①当b＞0时，函数f(x)在R上是单调增函数；

    ②当b＜0时，函数f(x)在R上有最小值；

    ③函数f(x)的图象关于(0，c)对称；

    ④方程f(x)＝0可能有三个实数根．

    [　　]

    A．①③

    B．①④

    C．①②④

    D．①③④

    查看答案和解析>>

    科目：高中数学 来源：2008年普通高等学校招生全国统一考试(天津卷)、数学(文) 题型：044

    设函数f(x)＝x4＋ax3＋2x2＋b(x∈R)，其中a，b∈R．

    (Ⅰ)当时，讨论函数f(x)的单调性；

    (Ⅱ)若函数f(x)仅在x＝0处有极值，求a的取值范围；

    (Ⅲ)若对于任意的a∈[－2，2]，不等式f(x)≤1在[－1，1]上恒成立，求b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设函数f(x)在x＝x0处的导数不存在，则曲线y＝f(x)


    1. A.
      在点[x0，f(x0)]处的切线不存在
    2. B.
      在点[x0，f(x0)]处的切线可能存在
    3. C.
      在点x0处不连续
    4. D.
      在x＝x0处连续

    查看答案和解析>>

    同步练习册答案