
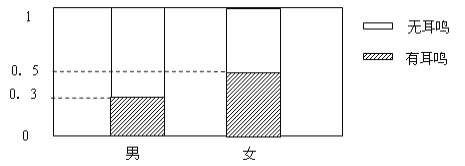
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附:![]()
![]()
【答案】①见解析;②能在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系.
【解析】试题分析:①由男女生各100人及等高条形图可知耳鸣的男生,耳鸣的女生的人数及无耳鸣的男生,无耳鸣的女生的人数,从而可绘出2×2列联表;
②由公式计算K2的观测值,与临界值比较,可得结论.
试题解析:
①由男女生各100人及等高条形图可知耳鸣的男生有100×0.3=30人,耳鸣的女生有100×0.5=50人
∴无耳鸣的男生有100-30=70人,
无耳鸣的女生有100-50=50人
所以2×2列联表如下:
有耳鸣 | 无耳鸣 | 总计 | |
男 | 30 | 70 | 100 |
女 | 50 | 50 | 100 |
总计 | 80 | 120 | 200 |
②由公式计算![]() 的观测值:
的观测值:
![]()
能在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系


科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为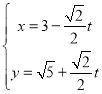 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程为
的方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于点
交于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明: ![]() <0.
<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有些家用电器(如冰箱等)使用了氟化物,氟化物的释放破坏了大气上层的臭氧层,使臭氧含量呈指数型函数变化,在氟化物排放量维持某种水平时,具有关系式Q=Q0e-0.0025t,其中Q0是臭氧的初始量.
(1)随着时间t的增加,臭氧的含量是增加的还是减少的?
(2)试估计多少年以后将会有一半的臭氧消失?(参考数据:ln 0.5=-0.69)
查看答案和解析>>
科目:高中数学 来源: 题型:
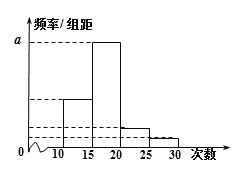
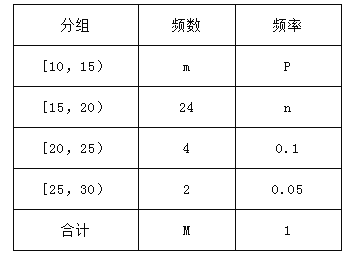
【题目】对某校高二年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高二学生有![]() 人,试估计该校高二学生参加社区服务的次数在区间
人,试估计该校高二学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于![]() 次的学生中任选
次的学生中任选![]() 人,求至多一人参加社区服务次数在区间
人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com