
[番茄花园1] .解析:本题主要考查函数的极值概念、导数运算法则、切线方程、导线应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识。
(Ⅰ)解:当a=1,b=2时,
因为f’(x)=(x-1)(3x-5)
故f’(2)=1
f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2
(Ⅱ)证明:因为f′(x)=3(x-a)(x-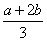 ),
),
由于a<b.
故a<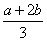 .
.
所以f(x)的两个极值点为x=a,x=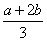 .
.
不妨设x1=a,x2=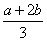 ,
,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b.
又因为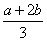 -a=2(b-
-a=2(b-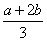 ),
),
x4=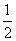 (a+
(a+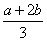 )=
)=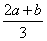 ,
,
所以a,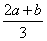 ,
,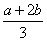 ,b依次成等差数列,
,b依次成等差数列,
所以存在实数x4满足题意,且x4=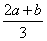 .
.
[番茄花园1]21.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com