
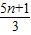 ,要使m,n都为整数,当且仅当n=3k-2∈N时,才满足m=5k-3∈N,代入求出x的值.⑤若函数f(x)在(-∞,+∞)上递增,且a+b≥0,则f(a)≥f(-b),f(b)≥f(-a),得出结论成立.
,要使m,n都为整数,当且仅当n=3k-2∈N时,才满足m=5k-3∈N,代入求出x的值.⑤若函数f(x)在(-∞,+∞)上递增,且a+b≥0,则f(a)≥f(-b),f(b)≥f(-a),得出结论成立.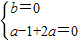 ,解得 a=
,解得 a= ,b=0,f(x)=x2+1,开口向下,③错误.
,b=0,f(x)=x2+1,开口向下,③错误.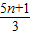


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届海南琼海市高二下学期第一次月考理科数学卷(解析版) 题型:填空题
下列五个命题:
①对于回归直线方程 ,
, 时,
时, .
.
②频率分布直方图中各小长方形的面积等于相应各组的频数.
③若 单调递增,则
单调递增,则 .
.
④样本 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 的平均值为
的平均值为 ,方差为
,方差为 .
.
⑤甲、乙两个乒乓球运动员进行乒乓球比赛,已知每一局甲胜的概率为0.6,乙胜的概率为0.4,比赛时可以用三局二胜或五局三胜制,相对于用五局三胜制,三局二胜制乙获胜的可能性更大.
其中正确结论的是 (填上你认为正确的所有序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题:①对于命题![]()
②![]() 是三个数a、G、b成等比数列的充要条件;
是三个数a、G、b成等比数列的充要条件;
③若函数![]() 是周期函数;
是周期函数;
④如果一组数据中,每个数都加上同一个非零常数,则这组数据的平均数和方差都改变。
其中正确命题的序号为 。(把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题:
①对于命题![]() ;
;
②![]() 是三个数a、G、b成等比数列的充要条件;
是三个数a、G、b成等比数列的充要条件;
③若函数![]() 是周期函数;
是周期函数;
④如果一组数据中,每个数都加上同一个非零常数,则这组数据的平均数和方差都改变.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
下列五个命题:
①对于回归直线方程![]() ,
,![]() 时,
时,![]() .
.
②频率分布直方图中各小长方形的面积等于相应各组的频数.
③若![]() 单调递增,则
单调递增,则![]() .
.
④样本![]() 的平均值为
的平均值为![]() ,方差为
,方差为![]() ,则
,则![]() 的平均值为
的平均值为![]() ,方差为
,方差为![]() .
.
⑤甲、乙两个乒乓球运动员进行乒乓球比赛,已知每一局甲胜的概率为0.6,乙胜的概率为0.4,比赛时可以用三局二胜或五局三胜制,相对于用五局三胜制,三局二胜制乙获胜的可能性更大.
其中正确结论的是 (填上你认为正确的所有序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com