
 或AB=
或AB=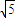 ;
;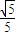 ;
;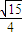 ;
; ;
; ;
; ;
;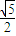 ;
;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
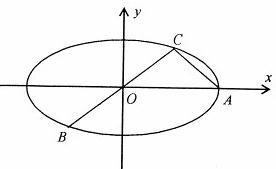 如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且
如图:已知椭圆A,B,C是长轴长为4的椭圆上三点,点A是长轴的一个端点,BC过椭圆的中心O,且| AC |
| BC |
| BC |
| AC |
| PQ |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
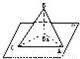
 如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.
如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.查看答案和解析>>
科目:高中数学 来源:湖南省长沙县实验中学2010届高三第一次月考理科数学试卷 题型:013
如图,已知一个多面体的平面展开图是由三个腰长为a的等腰三角形和一个边长为![]() 的正三角形组成,则该多面体的体积为
的正三角形组成,则该多面体的体积为
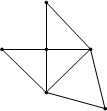
A.![]()
B.a3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年滨州市质检三文) (14分) 如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
(I)求椭圆的方程;
(II)求m的取值范围;
(III)求证直线MA、MB与x轴始终围成一个等腰三角形.

查看答案和解析>>
科目:高中数学 来源:2014届重庆市高二上学期期末考试文科数学试卷(解析版) 题型:解答题
如图,已知 是长轴为
是长轴为 的椭圆上三点,点
的椭圆上三点,点 是长轴的一个顶点,
是长轴的一个顶点,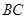 过椭圆中心
过椭圆中心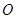 ,且
,且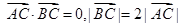 .
.
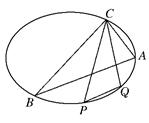
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上两点 使直线
使直线 与
与 轴围成底边在
轴围成底边在 轴上的等腰三角形,是否总存在实数
轴上的等腰三角形,是否总存在实数 使
使 ?请给出证明.
?请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com